3. Метод наименьших квадратов

Среднее арифметическое n чисел x₁, x₂, ..., x_n (которые здесь нет необходимости считать обязательно положительными) обладает замечательным минимальным свойством. Пусть и - числовое значение некоторой неизвестной величины, которое мы хотим определить насколько возможно точнее с помощью какого-то измерительного инструмента. Пусть произведено для этой цели n измерений, которые дали результаты x₁, x₂, ..., x_n, слегка различающиеся между собой, что обусловливается неизбежными и зависящими от разных причин измерительными ошибками. Возникает вопрос: какое же значение следует приписать величине u в качестве заслуживающего наибольшего доверия? Принято в качестве "истинного" или "оптимального" значения выбирать среднее арифметическое

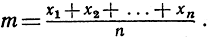
Дать подлинное обоснование указанной процедуре было бы невозможно, не углубляясь в пространные рассуждения, относящиеся к области теории вероятностей. Все же мы можем здесь отметить некоторое минимальное свойство средней арифметической m, которое до некоторой степени оправдывает ее выбор. Пусть u - какое-угодно числовое значение измеряемой величины. Тогда разности u - x₁, u - х₂, ..., u - х_n представляют собой отклонения этой величины от результатов отдельных наблюдений. Эти отклонения могут быть частью положительными, частью отрицательными, и совершенно естественно стремиться к такому оптимальному выбору u, при котором "тотальное" (в каком-то смысле) отклонение было бы возможно меньше. Следуя Гауссу, берут обыкновенно в качестве "измерителей неточности" не сами отклонения, а их квадраты (u - х_i)² и затем выбирают оптимальное значение и с таким расчетом, чтобы минимизировать "тотальное" отклонение, под каковым понимают сумму квадратов отдельных отклонений

Определенное таким образом оптимальное значение и есть не что иное, как, среднее арифметическое m: в этом заключается исходное положение знаменитого, созданного Гауссом "метода наименьших квадратов". Мы постараемся возможно проще доказать подчеркнутое выше утверждение. Если мы напишем

то получим

Сложим, далее, все такие равенства, полагая i = 1, 2, ..., n. Последний член при этом дает

а это выражение по определению m равно нулю. Следовательно, мы получаем:

Отсюда уже ясно, что

причем знак равенства возможен только при u = m. Как раз это самое мы и собирались доказать.

Общий метод наименьших квадратов принимает руководящий принцип - минимизировать сумму квадратов - во всех более сложных случаях, когда нужно как-то согласовать между собой ряд слегка противоречащих друг другу данных наблюдений. Так, представим себе, что измерены координаты х_i, y_i для n точек, которые, теоретически говоря, должны лежать на прямой линии, и предположим, что полученные таким эмпирическим путем точки оказываются расположенными по прямой не вполне точно. Как выбрать прямую, которая наилучшим образом была бы "приложена" или "подогнана" к этим точкам? Руководящий принцип приводит к следующему приему (который - необходимо признать - мог бы быть заменен и другими процедурами, основанными на иных рассуждениях). Пусть y = ах + b есть уравнение искомой прямой, так что наша проблема заключается в определении коэффициентов а и b. Измеренное по направлению оси у расстояние прямой от точки х_i, y_i равно y_i - (ax_i + b), т. е. y_i - ax_i - b, причем имеет положительный или отрицательный знак смотря по тому, расположена ли точка выше или ниже прямой. Тогда квадрат этого расстояния равен (y_i - ax_i - b)², и согласно основному принципу метода наименьших квадратов нам достаточно подобрать а и b таким образом, чтобы выражение

достигало наименьшего возможного значения. Мы приходим, таким образом, к минимальной проблеме с двумя переменными величинами а и b. Хотя решение этой проблемы с исследованием всех подробностей и не представляет особенной трудности, мы все же воздержимся здесь от его рассмотрения.