2. Обобщение на случай n переменных

Неравенство (1), связывающее средние арифметическое и геометрическое двух положительных величин, может быть обобщено на любое число n положительных величин, которые мы будем обозначать х₁, х₂, х₃, ..., х_n. Средним арифметическим этих величин называют величину

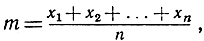
а средним геометрическим - величину

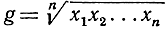
(здесь имеется в виду положительное значение радикала). Общая теорема утверждает, что

и что равенство g = m возможно только в том случае, если все величины х_i равны между собой.

Было предложено много различных остроумных доказательств этого общего результата. Простейший метод заключается в применении того же простого рассуждения, которое мы провели в пункте 1. Перед нами стоит проблема: разбить данное положительное число С на n положительных слагаемых, С = х₁ + х₂ + ... + x_n, таким образом, чтобы произведение Р = х₁х₂х₃...х_n было возможно большим. Мы будем исходить из допущения, на первый взгляд очевидного, но мы позднее будем иметь случай его проанализировать (§ 7), что наибольшее значение Р существует и достигается, скажем, при значениях х₁ = а₁, х₂ = а₂, ..., х_n = а_n. Нам достаточно установить, что а₁ = а₂ = ... = а_n, ибо в этом случае g = m. Допустим, что это не так: пусть, например, а₁≠а₂. Тогда рассмотрим значения

где

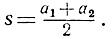
Мы заменим, другими словами, прежнюю систему значений величин х_i новой системой, которая отличается от прежней лишь тем, что значения двух первых величин х₁ и х₂ сделаны равными между собой, причем общая сумма С остается неизменной. Мы можем написать

где положено

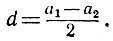
Новое произведение равно

тогда как прежнее произведение было

Отсюда ясно, что при d≠ 0

а это противоречит сделанному допущению, что произведение Р имеет максимальное значение. Итак, d = 0, и тогда а₁ = а₂. Таким же образом доказывается, что а₁ = а_i, где а_i обозначает любое из чисел а; отсюда следует, что все числа а равны между собой. Мы убедились в том, что 1) g = m, если все числа х_i равны между собой, 2) наибольшее значение g получается только тогда, когда все числа х_i равны между собой. Отсюда можно заключить, что во всех прочих случаях g < m. Теорема доказана.