1. Среднее арифметическое и среднее геометрическое двух положительных величин

Займемся прежде всего очень простой максимальной проблемой, с которой часто приходится встречаться и в самой математике, и в ее приложениях. В геометрической формулировке проблема эта заключается в следующем: среди всех прямоугольников с наперед заданным периметром найти тот, который имеет наибольшую площадь. Решением, как нетрудно догадаться, является квадрат. Доказать это можно следующим рассуждением. Пусть заданный периметр равен 2а. Тогда сумма х + y длин двух прилежащих сторон прямоугольника х и y равна постоянной величине а, а в максимум следует обратить произведение хy. "Среднее арифметическое" величин хну есть не что иное, как выражение

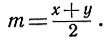
Введем еще величину

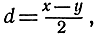
причем получатся соотношения

из них вытекает, что

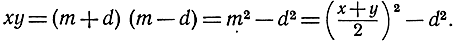
Так как d² не может быть отрицательно, а обращается в нуль только при х = y, то мы немедленно приходим к неравенству

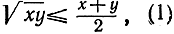
причем знак равенства здесь возможен только при d = 0, т. е. при х = y.

Так как х + y имеет постоянное значение а, то отсюда следует, что выражение √хy, а значит, и интересующая нас площадь хy принимают наибольшее возможное значение при х = y. Выражение

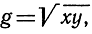
где радикал взят в арифметическом смысле - со знаком +, называется "средним геометрическим" положительных чисел х и y; неравенство (1) выражает основное соотношение между средними арифметическим и геометрическим.

Неравенство (1) вытекает также непосредственно из того факта, что выражение

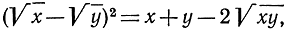
будучи точным квадратом, не может быть отрицательным и обращается в нуль только при х = y.

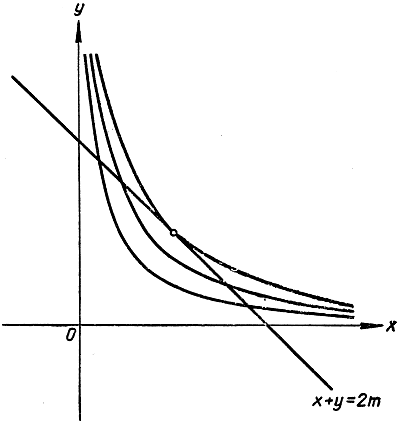
Рис. 221. Минимум хy при заданном значении х + y

Вот еще геометрический вывод того же неравенства. Рассмотрим в плоскости х, y неподвижную прямую линию х + y = 2m и вместе с ней семейство кривых (гипербол) хy = с, причем с постоянно для каждой кривой, но меняется при переходе от одной кривой к другой. Из рис. 221 ясно, что кривой, имеющей хоть одну общую точку с нашей прямой линией и соответствующей наибольшему значению с, является та гипербола, которая касается прямой в точке х = y = m; для этой гиперболы, следовательно, с = m². Итак,

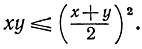
Следует заметить, что всякое неравенство вида f(x, y) ≤ g(x, y) можно прочесть двумя способами, и потому оно порождает как максимальное, так и минимальное свойства. Например, неравенство (1) выражает также тот факт, что среди всех прямоугольников с данной площадью именно квадрат имеет наименьший периметр.