5. Обобщение: проблема уличной сети

В проблеме Штейнера были заданы три точки А, В, С. Было бы естественно обобщить эту проблему на случай n заданных точек А₁, A₂, ..., А_n следующим образом: требуется найти в плоскости такую точку Р, чтобы сумма расстояний а₁ + а₂ + ... + а_n (где а_i обозначает расстояние РА_i) обращалась в минимум. (В случае четырех точек, расположенных так, как показано на рис. 215, в качестве Р нужно взять точку пересечения диагоналей четырехугольника А₁А₂, A₃A₄; пусть читатель проверит это в качестве упражнения.) Эта обобщенная проблема, также изученная Штейнером, не ведет к интересным результатам. В данном случае мы имеем дело с поверхностным обобщением, подобных которому немало встречается в математической литературе. Чтобы получить действительно достойное внимания обобщение проблемы Штейнера, приходится отказаться от поисков одной-единственной точки Р. Вместо того поставим задачей построить "уличную сеть" или "сеть дорог между данными деревнями", обладающую минимальной общей длиной. Точнее, даны n точек А₁, A₂, ..., А_n требуется найти такую связную систему прямолинейных отрезков, чтобы: 1) любые две из данных точек могли быть связаны ломаной линией, стороны которой входили бы в состав системы, 2) общая длина всей системы была наименьшей^*.

^* (Выработка общих методов для решения прикладных задач типа описанной составила в последние годы предмет так называемого линейного программирования; см., например, [45].)

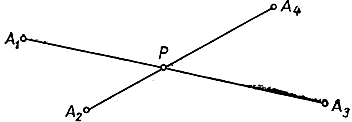
Рис. 215. Минимум суммы расстояний до четырех точек

Решение этой задачи имеет тот или иной вид в зависимости от расположения данных точек. Читатель с пользой сможет заняться более внимательным рассмотрением этого вопроса, исходя из проблемы Штейнера. Мы ограничимся здесь указанием результатов в типических примерах, изображенных на рис. 216-218. В первом примере решение дается системной из пяти отрезков с двумя "кратными точками", в которых сходятся по три сегмента, образуя между собой углы в 120°. Во втором примере число кратных точек равно трем. При некоторых иных расположениях данных точек указанные фигуры не получаются: возможны случаи "вырождения", когда какая-нибудь одна из данных точек (или несколько таких точек) становится сама "кратной точкой" сети - таков третий из приведенных примеров.

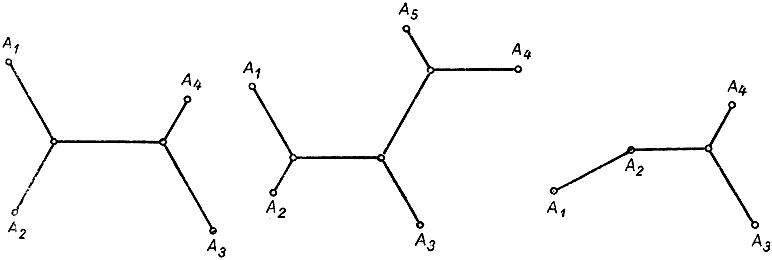
Рис. 216-218. Кратчайшая система путей, соединяющих данные точки

Если число данных точек равно n, то всего будет не более n-2 кратных точек, в которых сходятся по три отрезка, образуя углы в 120°.

Решение проблемы не всегда единственно. Так, если четыре данные точки расположены в вершинах квадрата, то возникает два эквивалентных решения (рис. 219, 220). Если точки А₁, А₂, ..., А_n являются вершинами ломаной линии с углами при вершинах, достаточно близкими к 180°, то сама ломаная является решением.

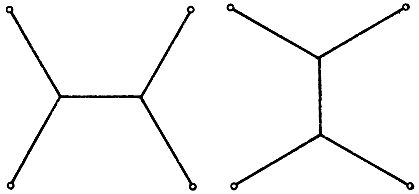
Рис. 219-220. Кратчайшие системы путей, соединяющих вершины квадрата