4. Замечания и упражнения

Из произвольной точки Р, взятой внутри равностороннего треугольника UVW, опустим перпендикуляры РА, РВ, PC на три стороны (рис. 214). Тогда точки A, В, С и Р образуют как раз такую фигуру, как мы рассматривали выше. Это замечание может быть использовано при решении проблемы Штейнера: достаточно, исходя из точек А, В, С, найти вершины равностороннего треугольника U, V, W.

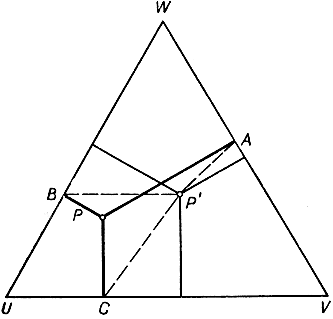
Рис. 214. Другое доказательство правильности решения Штейнера

Упражнения.

1. Выполнить указанное построение, основываясь на том обстоятельстве, что сумма трех перпендикуляров, опущенных на стороны из произвольной точки Р внутри равностороннего треугольника, постоянна, именно равна высоте треугольника.
2. Основываясь на аналогичном обстоятельстве в случае, когда Р находится вне UVW, исследовать дополнительную проблему. В трехмерном пространстве можно рассмотреть проблему, подобную штейнеровской: по заданным четырем точкам А, В, С, D найти такую пятую точку Р, чтобы сумма а + b + с + d обращалась в минимум.

^*Упражнение. Исследовать эту трехмерную проблему и дополнительную к ней методами § 1 или же пользуясь правильным тетраэдром.