3. Дополнительная проблема

Формальные математические методы нередко ведут дальше поставленных заранее целей. Так, если угол при вершине С больше 120°, то вместо точки Р (каковая совпадает на этот раз с точкой С) процедура геометрического построения дает другую точку Р'- ту, из которой наибольшая сторона треугольника А В видна под углом в 120°, а две другие стороны под углом в 60°. Конечно, точка Р' не дает решения рассматриваемой проблемы, но можно догадываться, что она имеет какое-то к ней отношение. Оказывается, в самом деле, что точка Р' решает следующую проблему: минимизировать выражение а + b - с. Доказательство, вполне аналогичное изложенному выше для случая выражения а + b + с и основанное на прямых результатах (§ 1, пункт 5), предоставляется в качестве упражнения читателю. Соединяя вместе полученные выводы, мы приходим к общей теореме.

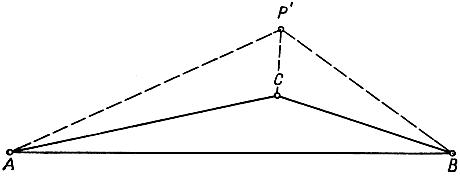
Рис. 213. Дополнительная проблема

Если все углы треугольника ABC меньше 120°, то сумма а + b + с расстояний а, b, с некоторой точки от точек А, В, С (соответственно) обращается в минимум в точке Р, из которой каждая из сторон видна под углом в 120°, а выражение а + b - с обращается в минимум в вершине С; если же один из углов, скажем С, больше 120°, то а + b + с минимизируется в точке С, а а + b - с - в точке Р', из которой две меньшие стороны треугольника видны под углом в 60°, а большая - под углом в 120°.

Таким образом, из двух минимальных проблем всегда одна решается построением окружностей, решение другой дается одной из вершин. В случае, когда ∠С = 120°, оба решения обеих проблем совпадают, так как точка, получаемая при геометрическом построении, оказывается вершиной С.