2. Анализ возникающих альтернатив

Чтобы установить, какая из двух возможностей имеет место, нам придется обратиться к построению точки Р. Для нахождения точки Р, из которой две стороны треугольника, например АС и ВС, видны под углом в 120°, достаточно через точки A, С провести такую окружность К₁, у которой меньшая из дуг АС содержала бы 120°, и через точки В, С провести окружность K₂, обладающую таким же свойством; затем взять точку пересечения двух дуг, содержащих по 120°, если только эти дуги действительно пересекаются. Из точки Р, таким образом найденной, сторона А В непременно также будет видна под углом в 120°, так как сумма трех углов с вершиной Р равна 360°.

Из рис. 210 видно, что если все три угла треугольника ABC меньше 120°, то две упомянутые дуги непременно пересекутся внутри треугольника. С другой стороны, если один из углов треугольника ABC, например С, больше, чем 120°, то дуги, о которых идет речь, не пересекутся (рис. 211). В этом случае не существует точки Р, из которой каждая из трех сторон треугольника ABC была бы видна под углом в 120°: окружности К₁ и К₂ пересекаются в точке Р', из которой стороны АС и ВС видны под углом в 60°, и только одна сторона AВ, противолежащая тупому углу, видна под углом в 120°.

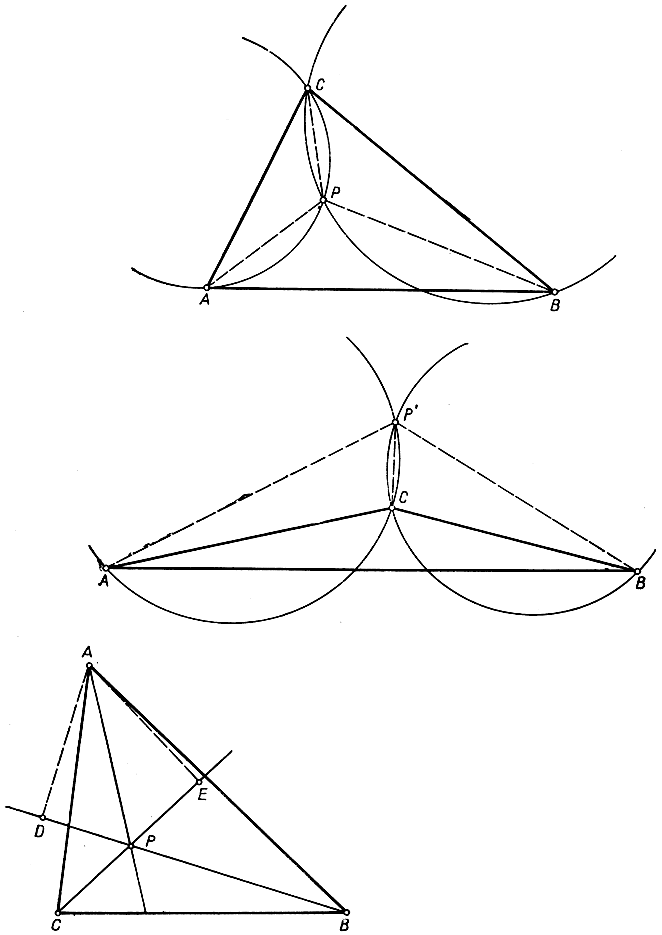
Рис. 210-212. К анализу различных возможностей в проблеме Штейнера

Если один из углов треугольника больше 120°, то, как мы только что видели, нет такой точки Р, из которой каждая из сторон видна под углом в 120°; значит, искомая точка (в которой достигается минимум) должна совпадать с одной из вершин (так как это на основании § 1 - единственная иная возможность), а именно, с вершиной тупого угла.

Если же у треугольника все углы меньше 120°, тогда, как мы видели, точку Р, из которой все стороны видны под углом в 120°, можно построить. Но, чтобы доказательство было закончено, нужно еще доказать, что для такой точки Р сумма а + b + с меньше, чем для любой из вершин треугольника (так как еще покамест неизвестно, которая из двух альтернатив в рассматриваемом случае имеет место). Итак, докажем, например, что а + b + с меньше, чем АВ + АС (рис. 212). С этой целью продолжим отрезок ВР и спроектируем точку А на полученную прямую; пусть найденная проекция есть D. Так как, очевидно, ∠APD = 60°, то длина проекции PD равна 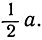Так как BD есть проекция АВ на прямую ВР, то, значит, BD<AB. Но 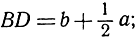поэтому 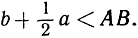Совершенно таким же образом, проектируя А на продолжение отрезка PC, мы убеждаемся, что 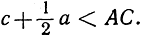Складывая два последних неравенства, получаем: a + b + c <AB + AC. Итак, искомая точка не может находиться в вершине А. Так как аналогично она не может находиться также в вершинах В или С, то, следовательно, найденная точка Р, из которой стороны видны под углом в 120°, решает задачу.