§ 5. Проблема Штейнера

1. Проблема и ее решение

Очень простая и вместе с тем поучительная проблема была изучена в начале прошлого столетия знаменитым берлинским геометром Якобом Штейнером. Требуется соединить три деревни А, В, С системой дорог таким образом, чтобы их общая протяженность была минимальной. В более точной математической формулировке: на плоскости даны три точки А, В, С; требуется найти такую четвертую точку Р, чтобы сумма a + b + с (где а, b, с - расстояния Р соответственно от А, В, С) обратилась в минимум. Решение проблемы таково: если в треугольнике ABC все углы меньше 120°, то в качестве точки Р следует взять ту, из которой все три стороны АВ, ВС, СА видны под углом в 120°; если же один из углов треугольника ABC, например С, больше или равен 120°, то точку Р нужно совместить с вершиной С.

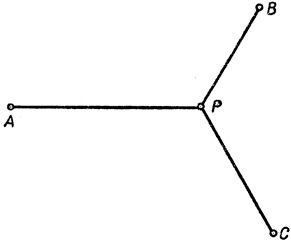
Рис. 208. Проблема Штейнера: РА + РВ + PC = minimum

Обосновать этот результат не представляет труда, если воспользоваться решением уже рассмотренных экстремальных задач. Предположим, что Р есть искомая точка. Возможны две альтернативы: или точка Р совпадает с одной из вершин А, В, С, или Р отлична от всех трех вершин. В первом случае очевидно, что Р должна быть вершиной именно самого большого угла С в треугольнике ABC, так как сумма СА + СВ меньше, чем сумма каких-нибудь двух других сторон треугольника ABC. Чтобы исчерпать вопрос, остается проанализировать второй возможный случай. Пусть К - окружность с центром С и радиусом с. Тогда точка Р должна быть расположена на К таким образом, что РА + РВ обращается в минимум. Если обе точки А и В вне К (как на рис. 209), то на основании § 1 отрезки РА и РВ должны образовывать одинаковые углы с окружностью К и, следовательно, с радиусом PC, который перпендикулярен к К. Так как это рассуждение можно повторить относительно окружности с центром А и радиусом а, то отсюда следует, что все углы, образованные отрезками РА, РВ, PC, равны между собой и, значит, каждый из них равен 120°, как и было сказано выше. Наше доказательство было построено на допущении, что обе точки А и В находятся вне круга К', докажем, что иначе быть не может. Пусть хотя бы одна из точек А, В, например А, находится внутри окружности К или на ней самой. Тогда АС≤с; так как, с другой стороны, при любом расположении точек А, В, Р сумма а + b ≥АВ, то a + b + с ≥ АВ + АС. Это последнее неравенство показывает, что наименьшее возможное значение суммы а + b + с получилось бы, если Р совпадает с А, что противоречит сделанному допущению, что Р отлично от A, В, С. Таким образом, доказано, что точки А и В находятся вне круга К. Точно таким же образом доказывается, что точки В, С находятся вне круга с центром А и радиусом а, а точки А, С - вне круга с центром В и радиусом b.

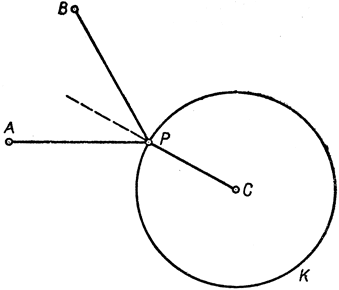
Рис. 209. К проблеме Штейнера