*5. Замечания, касающиеся задач на отражение и эргодическое движение

В динамике и в оптике представляется задачей первостепенной важности дать описание пути, или "траектории", частицы или светового луча в пространстве на протяжении неограниченного промежутка времени. Предполагая, что то или иное приспособление физически принуждает частицу или луч оставаться в некоторой ограниченной части пространства, особенно интересно установить, заполняет ли траектория в пределе эту часть пространства повсюду с приблизительно одинаковой "плотностью". Траектория, обладающая таким свойством, называется эргодической. Допущение существования эргодической траектории является исходной гипотезой для применения статистических методов в современных динамических и атомных теориях. Но известно лишь очень немного ситуаций, при которых может быть проведено строгое математическое доказательство этой "эргодической гипотезы".

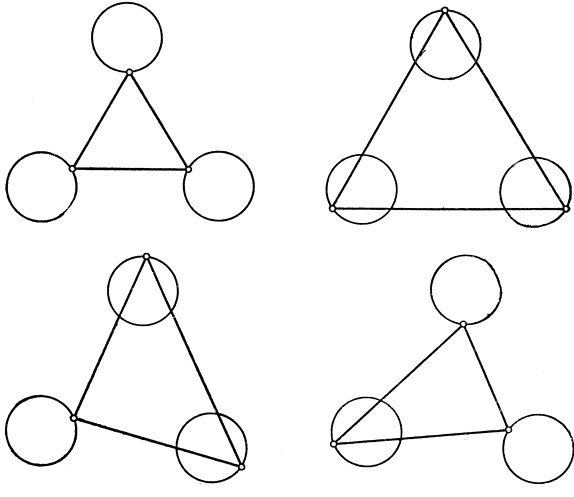
Рис. 204-207. Четыре типа световых треугольников между тремя кругами

Простейшие примеры относятся к случаю, когда движение происходит на плоскости внутри замкнутой кривой С, причем предполагается, что "стенка" С представляет собой математически совершенное зеркало, отражающее частицу (в остальном - свободную) под тем же углом, под каким она падает на стенку. Так, например, прямоугольный ящик - идеализированный биллиардный стол с совершенным отражением, причем рассматриваемая частица играет роль бильярдного шара,- обеспечивает, вообще говоря, эргодическое движение: идеальный "бильярдный шар" на протяжении бесконечного промежутка времени побывает в окрестности любой наперед заданной точки, если только исключить некоторые особые начальные положения и направления движения. Мы не приводим здесь доказательства, впрочем, не представляющего трудностей принципиального порядка.

Особенно любопытно движение на эллиптическом столе с фокусами F₁ и F₂. Так как касательная к эллипсу делает одинаковые углы с отрезками, проведенными из фокусов в точку касания, то каждая траектория, проходящая через один из фокусов, дает отражение, проходящее через другой фокус, и т. д. Нетрудно усмотреть, что после n отражений, независимо от начального положения, траектория при n неограниченно возрастающем будет приближаться к большой оси F₁F₂. Если начальный луч не проходит через фокус, то возникают две возможности. Или начальный луч проходит между фокусами: тогда все отраженные траектории будут проходить между фокусами, причем будут касательными к некоторой гиперболе с теми же фокусами F₁ и F₂. Или же начальный луч не разделяет фокусов: тогда этим же свойством будут обладать все отраженные лучи, причем все они будут касаться некоторого эллипса с теми же фокусами F₁ и F₂. Таким образом, движение внутри эллипса ни при каких начальных условиях не оказывается эргодическим.

Упражнения.

1. Доказать, что если начальный луч проходит через какой-нибудь фокус эллипса, то его n-е отражение при неограниченном возрастании n стремится к большой оси.
2. Доказать, что если начальный луч проходит между фокусами эллипса, то этим же свойством обладают все отраженные лучи, и все они касательны к некоторой гиперболе с фокусами F₁ и F₂; точно так же, если начальный луч не проходит между фокусами, то этим же свойством обладают все отраженные лучи, и все они касательны к некоторому эллипсу с фокусами F₁ и F₂. (Указание. Установите, что до отражения и после отражения в точке R луч делает соответственно одинаковые углы с отрезками RF₁ и RF₂; потом докажите, что софокусные конические сечения характеризуются отмеченным обстоятельством.)