3. Тупоугольные треугольники

В обоих предшествующих доказательствах предполагалось, что все три угла А, В, С острые. Если бы, скажем, угол С был тупой (рис. 202), то точки Р и Q лежали бы вне треугольника. Поэтому, строго говоря, высотный треугольник уже нельзя было бы считать вписанным в данный, если только мы не условимся заранее называть вписанным такой треугольник, вершины которого лежат на сторонах данного треугольника или на их продолжениях. Как бы то ни было, высотный треугольник в расширенном смысле не обладает минимальным периметром, так как PR>CR, QR>CR и, значит, р = PR + QR + PQ > 2CR. Так как рассуждение в первой части последнего доказательства показывает, что минимальный периметр - если только он не дается высотным треугольником - должен быть равен одной из удвоенных высот, то отсюда легко заключить, что в случае тупоугольного треугольника "вписанный треугольник" с наименьшим периметром есть не что иное, как высота, опущенная из вершины тупого угла, учитываемая в обоих направлениях; хотя треугольника в собственном смысле здесь и нет, однако можно все же указать настоящие вписанные треугольники, периметры которых как угодно мало отличаются от удвоенной высоты. В промежуточном случае, когда данный треугольник прямоугольный, оба решения (высотный треугольник и удвоенная высота, опущенная из прямого угла) совпадают.

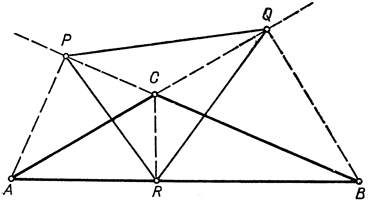
Рис. 202. Высотный треугольник в тупо угольном треугольнике

Не лишен интереса вопрос о том, не обладают ли каким-нибудь экстремальным свойством высотные треугольники данных тупоугольных треугольников. Не имея возможности подробно рассматривать этот вопрос, отметим лишь, что такие высотные треугольники не обращают в минимум сумму сторон р + q + r, но зато обеспечивают стационарное значение типа минимакса для выражения вида р + q - r, где r - та сторона вписанного (в расширенном смысле) треугольника, которая соответствует тупому углу.