2. Другое доказательство

Следующее решение задачи Шварца является, вероятно, самым простым. Оно основывается на теореме, ранее доказанной в этой главе: если точки Р и Q лежат по одну сторону прямой L (но не на ней самой), то сумма расстояний PR + RQ, где R - точка на L, обращается в минимум в том случае, если PR и OR делают одинаковые углы с L. Пусть треугольник PQR, вписанный в данный треугольник ABC, решает поставленную минимальную задачу. Тогда точка R на стороне АВ должна быть такой, чтобы сумма PR+QR была наименьшей, следовательно, углы ARQ и BRP должны быть равны; и точно так же ∠AQR = =∠CQP, ∠BPR = ∠CPQ. Таким образом, для искомого треугольника с минимальным периметром - если только таковой существует - должно быть выполнено то же самое свойство равенства углов, каким обладает высотный треугольник. Остается показать, что при таком условии наш треугольник не может отличаться от высотного. Кроме того, так как в теореме, на которую мы ссылались, предполагается, что Р и Q не лежат на АВ, то доказательство не годится для случая, когда одна из точек Р, Q, R совпадает с какой-нибудь вершиной данного треугольника (при этом периметр треугольника выродился бы в удвоенную соответствующую высоту); чтобы доказательство было исчерпывающим, нужно еще установить, что периметр высотного треугольника меньше любой из удвоенных высот данного треугольника.

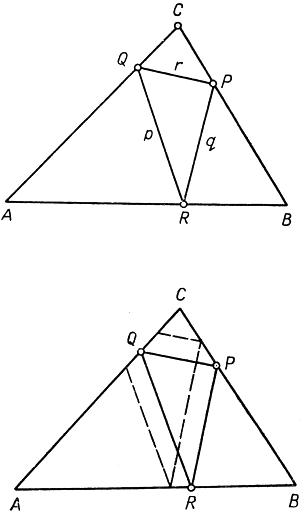
Рис 199-200. Другое доказательство минимального свойства высотного треугольника

Обращаясь сначала к первому пункту, заметим, что если вписанный треугольник обладает указанным выше свойством равенства углов, то рассматриваемые углы при вершинах Р, Q и R соответственно равны углам A, B и С. В самом деле, допустим, например, что ∠ARQ = ∠BRP = ∠С + δ. Тогда, применяя теорему о сумме углов треугольника к треугольникам ARQ и BRP, мы видим, что углы при Q должны равняться В - δ, а углы при Р должны равняться А - δ. Но тогда сумма углов треугольника CPQ равна (А - δ) + (В - δ) + С = 180° - 2δ; с другой стороны, она же равна 180°. Поэтому δ = 0. Мы уже видели, что высотный треугольник обладает отмеченным свойством. Всякий иной вписанный треугольник, обладающий тем же свойством, имел бы стороны, соответственно параллельные сторонам высотного треугольника; другими словами, он был бы ему подобен и подобно расположен. Читатель докажет самостоятельно, что, кроме самого высотного треугольника, другого такого треугольника не существует (рис. 200).

Покажем, наконец, по-прежнему ограничиваясь случаем остроугольного треугольника, что периметр высотного треугольника меньше, чем любая удвоенная высота данного треугольника. Проведем прямые QP и QR и затем из вершины В (рис. 201) опустим перпендикуляры на прямые QP, QR и PR; пусть L, М и N - основания этих перпендикуляров. Так как отрезки QL и QM являются проекциями высоты QB на прямые QP и QR,' то QL + QM<2QB. Но QL + QM = p, где через р обозначен периметр высотного треугольника. Действительно, треугольники MRB и NRB равны, так как ∠MRB = ∠NRB, а углы при вершинах М и N прямые. Значит, RM = RN, и поэтому QM = QR + RN. Точно также мы убеждаемся,что PN = PL и, следовательно, QL = QP + PN. Отсюда вытекает: QL + QM = QP + PN + QR + RN = QP + PR + RQ = p. Но раньше было показано, что 2QB>QL + QM. Итак, р меньше, чем удвоенная высота QB. Это же рассуждение может быть применено и к каждой из двух других высот. Таким образом, минимальное свойство высотного треугольника доказано полностью.

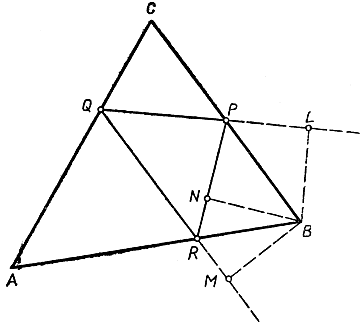
Рис. 201. К доказательству минимального свойства высотного треугольника

Между прочим, приведенное построение позволяет непосредственно вычислить р. Мы знаем, что углы РQC и ROA равны углу В, так что ∠РQB = ∠RQB = 90° - В и cos ∠PQB = sin В. Отсюда следует с помощью элементарных тригонометрических соображений, что QM = QL = QB sin В и p = 2QB sin B. Таким же образом можно показать, что р = 2РA sin А = 2RC sin С. Из тригонометрии известно, что RC = a sin В = b sin A и т. д., откуда следует: р = 2а sin В sin С = 2b sin С sin A = 2с sin A sin B. И наконец, вводя радиус описанного круга r и принимая во внимание, что а = 2r sin A, b = 2r sin В, с = 2r sin С, мы получим симметрическую формулу