§ 4. Треугольник Шварца

1. Доказательство, предложенное Шварцем

Герман Амандус Шварц (1843-1921), выдающийся математик, профессор Берлинского университета, сделал многое для развития современной теории функций и анализа. Он не считал ниже своего достоинства писать на темы элементарного содержания, и одна из его работ посвящена следующей задаче: в данный остроугольный треугольник вписать другой треугольник с минимальным периметром. (Говоря, что некоторый треугольник вписан в данный, мы подразумеваем, что на каждой из сторон данного треугольника имеется вершина рассматриваемого треугольника.) Мы убедимся в дальнейшем, что существует только один искомый треугольник: именно, его вершинами являются основания высот данного треугольника. Такой треугольник условимся называть высотным треугольником.

Шварц доказал минимальное свойство высотного треугольника, применяя метод отражения и основываясь на следующей теореме элементарной геометрии: В каждой из вершин Р, Q, R (рис. 197) две стороны высотного треугольника делают одинаковые углы со стороной данного треугольника, именно каждый из этих углов равен углу при противоположной вершине данного треугольника. Например, углы ARQ и BRP равны каждый углу С и т. д.

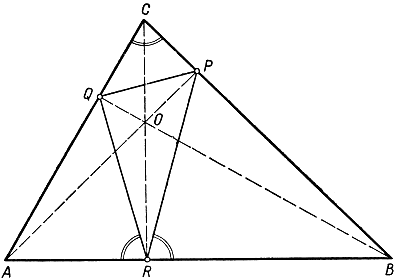
Рис. 197. Высотный треугольник в треугольнике AВС

Докажем прежде всего эту теорему. Так как углы ОРВ и ORB прямые, то около четырехугольника OPBR можно описать окружность. Следовательно, ∠PBO = ∠PRO, так как названные углы опираются на одну и ту же дугу описанной окружности. Но угол РВО дополнительный к углу С, так как треугольник CBQ прямоугольный, а угол PRO дополнительный к углу PRB. Поэтому ∠PRB = ∠C. Таким же образом, рассуждая по поводу четырехугольника QORA, заключаем, что ∠QRA = ∠C и т. д.

Этот результат приводит к следствию, относящемуся к высотному треугольнику: так как, например, ∠AQR = ∠CQP, то при отражении относительно стороны АС данного треугольника сторона RQ направляется по стороне PQ, и обратно. Аналогично для других сторон.

Перейдем теперь к доказательству минимального свойства высотного треугольника. В треугольнике ABC рассмотрим, наряду с высотным треугольником, какой-нибудь другой вписанный треугольник, скажем, UVW. Отразим всю фигуру сначала относительно стороны АС треугольника ABC, затем вновь получившуюся фигуру отразим относительно стороны АВ, потом - относительно ВС, потом - относительно АС и, наконец, относительно АВ. Таким образом мы получим всего шесть конгруэнтных треугольников, причем в каждом из них будет заключен высотный треугольник и еще другой вписанный треугольник (рис. 198). Сторона ВС последнего треугольника параллельна стороне ВС первого треугольника. В самом деле, при первом отражении сторона ВС поворачивается отражении сторона UL поворачивается по часовой стрелке на угол 2С, затем опять по часовой стрелке на угол 2В, при третьем отражении - остается неизменной; при четвертом - поворачивается на угол 2С против часовой стрелки и при пятом - на угол 2В опять против часовой стрелки. Итого, общий угол поворота равен нулю.

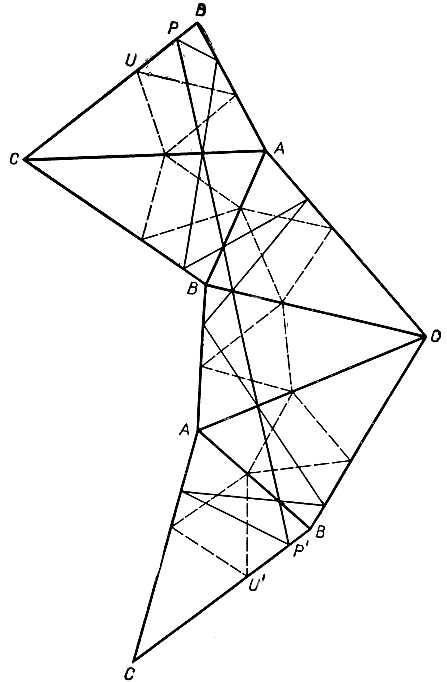
Рис. 198. Доказательство минимального свойства высотного треугольника, данное Шварцем

Благодаря указанному выше свойству высотного треугольника прямолинейный отрезок РР' равен удвоенному периметру треугольника PQR: действительно, РР' составляется из шести отрезков, по очереди равных и первой, второй и третьей стороне PQR, причем каждая из сторон входит дважды. Таким же образом ломаная линия, соединяющая U и U' имеет длину, равную удвоенному периметру треугольника UVW. Эта ломаная не короче, чем прямолинейный отрезок UU'. Что же касается прямолинейного отрезка UU', то он равен РР' так как отрезок UU' параллелен РР'. Значит, ломаная линия UU' не короче, чем прямая РР', т. е. периметр высотного треугольника не больше, чем периметр любого другого треугольника, вписанного в данный. Это и нужно было доказать. Итак, установлено, что минимум существует и что он реализуется в случае высотного треугольника. Что нет иного вписанного треугольника с тем же периметром - это, однако, не доказано, и это мы докажем дальше.