4. Расстояние точки от поверхности

Для расстояний точки Р от различных точек замкнутой кривой существуют (по меньшей мере) два стационарных значения: минимальное и максимальное. При переходе к трем измерениям не обнаруживается никаких новых фактов, если мы ограничимся рассмотрением такой поверхности С, которая топологически эквивалентна сфере (как, например, эллипсоид). Но если поверхность рода 1 или более высокого, то дело обстоит иначе. Рассмотрим поверхность тора С. Какова бы ни была точка Р, всегда, конечно, существуют на торе С точки, дающие наибольшее и наименьшее расстояние от Р, причем соответствующие отрезки перпендикулярны к самой поверхности. Но мы сейчас установим, что в этом случае существуют и точки минимакса. Вообразим на торе один из "меридианных" кругов L (рис. 195) и на этом круге L найдем точку Q, ближайшую к Р. Затем, перемещая круг L по тору, найдем такое его положение, чтобы расстояние PQ стало: а) минимальным - тогда получается точка на С, ближайшая к Р; b) максимальным-тогда получится стационарная точка минимакса. Таким же образом мы могли бы найти на L точку, наиболее удаленную от Р, и затем искать положение L, при котором найденное наибольшее расстояние было бы: с) максимальным (получится точка на С, наиболее удаленная от Р); d) минимальным. Итак, мы получим четыре различных стационарных значения для расстояния точки тора С от точки Р.

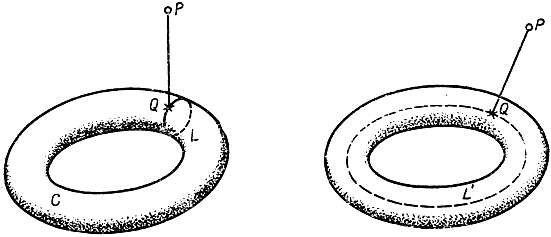
Рис. 195-196. Расстояние от точки до поверхности

*Упражнение. Повторить то же рассуждение для иного типа L' замкнутой кривой на С, которая также не может быть стянута в точку (рис. 196).