3. Точки минимакса и топология

Существует глубокая связь между общей теорией стационарных точек и топологическими идеями. По этому поводу мы можем здесь дать только краткое указание и ограничимся рассмотрением одного примера.

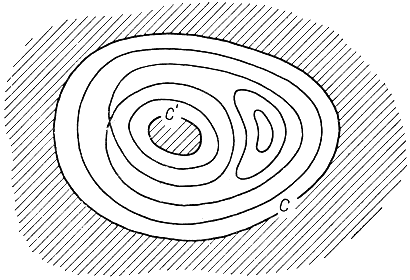
Рис. 194. Стационарные точки в двусвязной области

Рассмотрим горный ландшафт на кольцеобразном острове В с двумя береговыми контурами С и С', если обозначим, как раньше, высоту над уровнем моря через u = f(x, y), причем допустим, что f(x, y) = 0 на контурах С и С' и f(x, y)>0 внутри, то на острове должен существовать по меньшей мере один горный перевал: на рис. 194 такой перевал находится в точке, где пересекаются две линии уровня. Справедливость высказанного утверждения становится наглядной, если мы поставим своей задачей найти такой путь, соединяющий С и С', который не поднимался бы на большую высоту, чем это неизбежно. Каждый путь от С к C' имеет наивысшую точку, и если мы выберем такой путь, для которого наивысшая точка оказывается самой низкой, то полученная таким образом наивысшая точка и будет седловой точкой функции u = f(x, y). (Следует оговорить представляющий исключение тривиальный случай, когда некоторая горизонтальная плоскость касается кольцеобразного горного хребта по замкнутой кривой.) В случае области, ограниченной р замкнутыми кривыми, вообще говоря, должна существовать не менее чем р-1 точек минимакса. Подобного же рода соотношения, как установил Марстоя Морз, имеют место и для многомерных областей, но разнообразие топологических возможностей и типов стационарных точек в этом случае значительно большее. Эти соотношения образуют основу современной теории стационарных точек.