§ 3. Стационарные точки и дифференциальное исчисление

1. Экстремальные и стационарные точки

В предшествующих рассуждениях мы совсем не пользовались техническими приемами дифференциального исчисления.

Трудно не признать, что наши элементарные методы являются более простыми и более прямыми, чем методы анализа. Вообще, занимаясь той или иной научной проблемой, лучше исходить из ее индивидуальных особенностей, чем полагаться исключительно на общие методы, хотя, с другой стороны, общий принцип, уясняющий смысл применяемых специальных процедур, конечно, всегда должен играть руководящую роль. Таково именно значение методов дифференциального исчисления при рассмотрении экстремальных проблем. Наблюдаемое в современной науке стремление к общности представляет только одну сторону дела, так как то, что в математике является подлинно жизненным, без всякого сомнения обусловливается индивидуальными чертами рассматриваемых , проблем и применяемых методов.

В своем историческом развитии дифференциальное исчисление в весьма значительной степени испытало воздействие индивидуальных проблем, связанных с разысканием наибольших и наименьших значений величин. Связь между экстремальными проблемами и дифференциальным исчислением можно уяснить себе следующим образом. В главе VIII мы займемся обстоятельным изучением производной f'(x) от функции f(x) и ее геометрического смысла. Там мы увидим, что, говоря кратко, производная f'(x) есть наклон касательной к кривой y = f(x) в точке (х, y). Геометрически очевидно, что в точках максимума или минимума гладкой кривой y = f(x) касательная к кривой непременно должна быть горизонтальной, т. е. наклон должен равняться нулю. Таким образом мы получаем для точек экстремума условие f'(x) = 0.

Чтобы отдать себе ясно отчет в том, что означает обращение в нуль производной f'(x), рассмотрим кривую, изображенную на рис. 191. Мы видим здесь пять точек А, В, С, D, ?, в которых касательная к кривой горизонтальна; обозначим соответствующие значения f(x) в этих точках через а, b, с, d, е. Наибольшее значение f(x) (в пределах области, изображенной на чертеже) достигается в точке D, наименьшее - в точке A. В точке В имеется максимум - в том смысле, что во всех точках некоторой окрестности точки В значение f(x) меньше, чем b, хотя в точках, близких к D, значение f(x) все же больше, чем b. По этой причине принято говорить, что в точке В имеется относительный максимум функции f(x), тогда как в точке D - абсолютный максимум. Точно так же в точке С имеет место относительный минимум, а в точке А - абсолютный минимум. Наконец, что касается точки Е, то в ней нет ни максимума, ни минимума, хотя в ней все же осуществляется равенство f'(x) = Q, Отсюда следует, что обращение в нуль производной f'(x) есть необходимое, но никак не достаточное условие для появления экстремума гладкой функции f(x); другими словами, во всякой точке, где имеется экстремум (абсолютный или относительный), непременно имеет место равенство f'(x) = 0, но не во всякой точке, где f'(x) = 0, обязан быть экстремум. Те точки, в которых производная f'(x) обращается в нуль, независимо от того, имеется ли в них экстремум, называются стационарными. Дальнейший анализ приводит к более или менее сложным условиям, касающимся высших производных функции f(x) и полностью характеризующим максимумы, минимумы и иные стационарные точки.

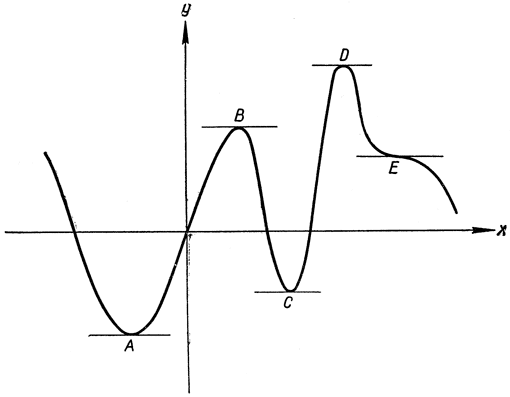
Рис. 191. Стационарные точки функции