2. Примеры

Легко понять, что ранее полученные результаты являются частным случаем этой общей теоремы. Если речь идет об экстремуме суммы р + q, то функция f(x, y) есть р + q, а кривые f(x, y) = с - софокусные эллипсы с фокусами Р и Q. В согласии с общей теоремой эллипсы, проходящие через те точки кривой С, где достигается экстремум одного или другого вида, касаются кривой С в этих точках. Если речь идет об экстремуме разности р - q, то функция f(х, y) есть р - q, и тогда кривые f(x, y) = с - софокусные гиперболы с фокусами Р и Q: и в этом случае гиперболы, проходящие через точки, где достигается экстремум, касаются кривой С.

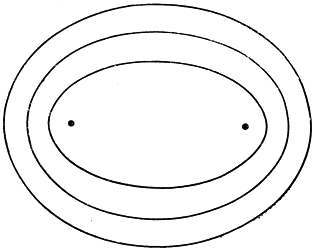
Рис. 188. Софокусные эллипсы

Вот еще пример задачи того же типа. Дан отрезок прямой PQ и прямая l, его не пересекающая; требуется установить: из какой точки прямой l отрезок PQ виден под наибольшим углом?

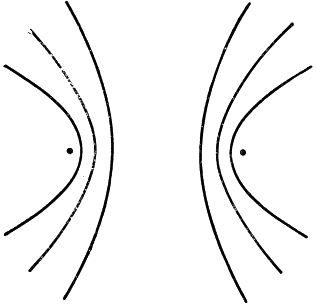
Рис. 189. Софокусные гиперболы

Функция, максимум которой надлежит определить в этой задаче, есть угол θ, под которым из точки, движущейся по прямой l, виден отрезок РQ; если R - какая угодно точка плоскости с координатами х, y, то угол, под которым отрезок PQ виден из R, есть функция θ = f(x, y) от переменных х, y. Из элементарной геометрии известно, что семейство кривых θ - f(x, y) = const состоит из окружностей, проходящих через Р и Q, так как хорда круга видна под одним и тем же углом из всех точек дуги окружности, расположенной по одну сторону хорды. Из рис. 190 видно, что, вообще говоря, имеются две окружности рассматриваемого семейства, касающиеся прямой l: их центры расположены по разные стороны отрезка PQ. Одна из точек касания дает абсолютный максимум величины θ, тогда как другая - лишь "относительный" максимум: это значит, что значения θ в этой точке больше, чем значения в некоторой окрестности рассматриваемой точки. Больший из двух максимумов - абсолютный максимум - дается той точкой касания, которая расположена в остром угле, образованном прямой l и продолжением отрезка PQ, а меньший - той точкой касания, которая расположена в тупом угле, образованном этими прямыми. (Точка пересечения прямой l с продолжением отрезка PQ дает минимальное значение угла θ - именно θ = 0.)

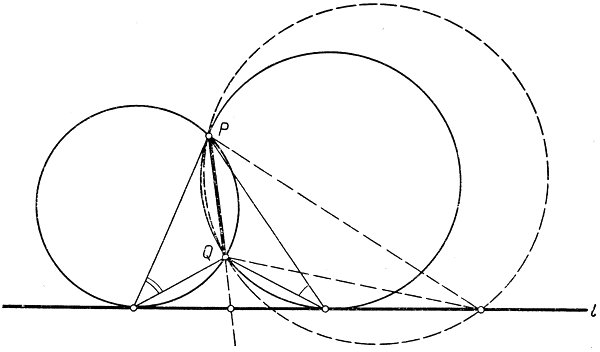
Рис. 190. Из какой точки прямой l отрезок PQ виден под наибольшим углом?

Обобщая рассмотренную задачу, мы можем заменить прямую l какой-нибудь кривой с и искать точки R на кривой с, из которых данный отрезок PQ, не пересекающий с, виден под наибольшим или наименьшим углом. В этой задаче, как и в предыдущей, окружность, проходящая через Р, Q и R, должна в точке R касаться кривой с.