§ 2. Общий принцип, которому подчинены экстремальные задачи

1. Принцип

Предыдущие задачи являются частными случаями некоторой общей проблемы, которую удобнее всего сформулировать аналитически. Возвращаясь к первой из рассмотренных задач, касающейся суммы р + q, мы видим, что она заключается в том, чтобы, обозначив через х, y координаты точки R, через х₁, y₁ координаты точки Р и через х₂, y₂ координаты точки Q, найти экстремальные значения функции

где положено

Рассматриваемая функция непрерывна во всей плоскости, но точка R с координатами х, y подчинена требованию находиться на кривой С. Эта последняя кривая, допустим, определена уравнением g(x, y) = 0; например, уравнением х² + y² - 1 = 0, если С - единичная окружность.

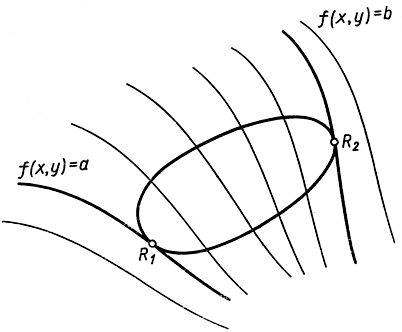
Рис. 187. Экстремумы функции на кривой

Обратимся теперь к общей задаче: найти экстремальные значения некоторой данной функции f (x, y), если переменные х и y подчинены условию g(x, y) = 0. Постараемся характеризовать решение этой задачи. Для этого рассмотрим семейство кривых f (x, y) = с; при этом под "семейством" кривых понимаем совокупность всех кривых, определяемых указанным уравнением при различных значениях постоянной с (но такое значение неизменно для всех точек каждой кривой в отдельности). Предположим, что через каждую точку плоскости - или по крайней мере некоторой ее части, содержащей кривую С,- проходит одна и только одна кривая семейства f (x, y) = с. Тогда при непрерывном увеличении с кривая f(x, y) = с "заметает" некоторую часть плоскости, однако при этом ни одну точку не "заметает" дважды. (Примеры такого рода семейств: х² - y² = c, х + y = с, х = с.) В частности, одна кривая рассматриваемого семейства пройдет через точку R₁, в которой f (x, y) принимает наибольшее значение на кривой С, и другая - через точку R₂, в которой f (x, y) принимает наименьшее значение на С. Пусть наибольшее значение есть а, наименьшее - Ь. По одну сторону кривой f(x, y) = а значение f(x, y) меньше, чем а, по другую - больше, чем а. Так как на кривой С имеет место неравенство f(х, y) ≤ а, то кривая С должна целиком лежать по одну и ту же сторону кривой f(x, y) = а; отсюда следует, что она в точке R₁ касается кривой f(x, y) = а. Точно так же кривая С касается в точке R₂ кривой f(x, y) = b.

Итак, доказана общая теорема: Если в точке R на кривой С функция f(x, y) имеет экстремальное значение а, то кривая f(x, y) = а в точке R касается кривой С.