* 5. Экстремальные расстояния точки от данной кривой

Начнем с того, что определим наибольшее и наименьшее расстояния данной точки Р от точек данной кривой С. Предположим для простоты, что С есть простая замкнутая кривая, имеющая всюду касательную (рис. 184). Понятие касательной к кривой, принимаемое здесь на интуитивной основе, будет подвергнуто анализу в следующей главе. Ответ очень прост: если для некоторой точки R на С расстояние PR достигает минимума или максимума, то прямая PR непременно перпендикулярна к касательной к С в точке R, короче говоря, прямая PR перпендикулярна к С. Доказательство вытекает из следующего обстоятельства: окружность с центром Р, проходящая через R, должна быть касательной к кривой С. Действительно, если R есть точка наименьшего расстояния, то кривая С должна целиком лежать вне круга и поэтому в точке R не может его пересекать; если же R есть точка наибольшего расстояния, то С должна целиком лежать внутри круга и потому опять-таки в точке R пересекать его не может. (Это следует из того очевидного факта, что расстояние некоторой точки от Р меньше, чем RP, если эта точка - внутри круга, и больше, чем RP, если она - вне его.) Итак, окружность и кривая касаются в точке R, и касательная у них в этой точке - одна и та же. Остается заметить, что отрезок PR как радиус окружности перпендикулярен к касательной к окружности в точке R и, следовательно, к самой кривой С в той же точке.

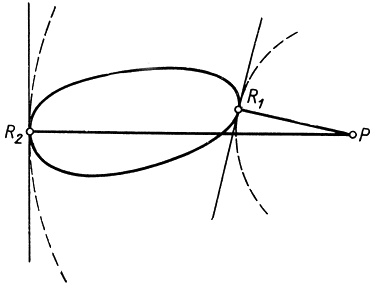
Рис. 184. Экстремальные расстояния от точек кривой

В теснейшей связи с предыдущим стоит следующее предложение, доказательство которого предоставляется читателю: диаметр замкнутой кривой С (т. е. наибольшая из ее хорд) в своих концах обязательно перпендикулярен к С. Аналогичное утверждение можно сформулировать и доказать для трехмерного случая.

Упражнение. Доказать, что наикратчайший и наидлиyнейший отрезки, связывающие две взаимно непересекающиеся замкнутые кривые, перпендикулярны в своих концах к самим кривым.

Можно обобщить и задачи пункта 4, касающиеся суммы и разности расстояний. Рассмотрим вместо прямой линии L простую замкнутую кривую С, обладающую касательной в каждой точке, и еще две точки Р и Q, не лежащие на С. Постараемся характеризовать те точки на кривой С, для которых сумма р + q или разность р - q принимает экстремальные значения (причем р и q обозначают соответственно расстояния переменной точки на С от точек Р и Q). Теперь уже нельзя применить то простое, основанное на отражении построение, с помощью которого мы решили обе задачи в случае, когда С была прямой линией. Но мы можем воспользоваться для поставленной здесь цели свойствами эллипса и гиперболы. Так как С на этот раз - замкнутая кривая, а не линия, уходящая в бесконечность, то и максимум и минимум на ней действительно реализуются: в самом деле, можно не подвергать сомнению то обстоятельство, что величины р + q и р - q достигают и наибольшего, и наименьшего значений на всяком конечном сегменте кривой, следовательно, на замкнутой кривой (см. §7).

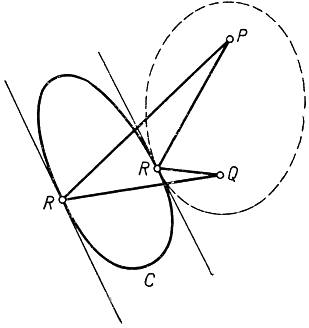
Рис. 185. Максимум и минимум суммы PR + QR

Останавливаясь на случае суммы р + q, предположим, что R - та точка на С, в которой имеет место максимум; пусть 2а есть значение р + q в этой точке. Рассмотрим эллипс с фокусами Р и Q - геометрическое место точек, для которых р + q = 2а. Этот эллипс в точке R должен касаться кривой С (доказательство предоставляется читателю в качестве упражнения). Но мы видели, что отрезки PR и QR делают одинаковые углы с эллипсом в точке R, и так как эллипс в точке R касается кривой С, то отрезки PR и QR делают в той же точке также одинаковые углы и с С. Совершенно аналогичное рассуждение приводит нас к тому же результату и в случае, если в точке R сумма р + q обращается в минимум.

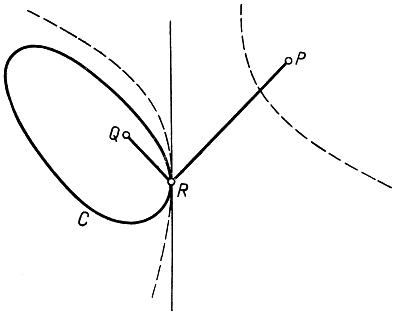
Рис. 186. Минимум разности PR - QR

Итак, мы пришли к теореме: Дана замкнутая кривая С и две точки, Р и Q вне ее; тогда в каждой из точек R, в которых сумма р + q принимает наибольшее или наименьшее значение на кривой С, отрезки PR и QR делают одинаковые углы с самой кривой (т. е. с ее касательной).

Если точка Р - внутри С, а точка Q - вне С, то теорема остается справедливой для той точки, где р + q принимает наибольшее значение, но она теряет смысл для точки, где р + q принимает наименьшее значение, так как эллипс вырождается в отрезок прямой.

Рассуждая аналогичным образом (воспользовавшись вместо свойств эллипса свойством гиперболы), читатель сможет доказать следующую теорему: Дана замкнутая кривая С и две точки Р и Q - одна внутри, другая вне С; тогда в каждой из тех точек R на С, где разность р - q принимает наибольшее или наименьшее значение, отрезки PR и QR делают одинаковые углы с самой кривой С. Но нужно вместе с тем отметить, что между случаем, когда С - прямая, и случаем, когда С - замкнутая кривая, есть существенное различие: в первом случае приходится разыскивать максимум абсолютного значения разности, т. е. максимум |р - q|, тогда как во втором сама разность р - q достигает и наибольшего, и наименьшего значений.