4. Свойства касательных к эллипсу и гиперболе. Соответствующие экстремальные свойства

С теоремой Герона связаны некоторые важные геометрические задачи. Мы установили, что если R - такая точка на прямой L, что PR + RQ обращается в минимум, то прямые PR и RQ образуют одинаковые углы с L. Обозначим минимальное значение PR + RQ через 2а. Пусть, с другой стороны, р и q обозначают расстояния произвольной точки плоскости соответственно от точек Р и Q; рассмотрим геометрическое место всех точек плоскости, для которых p + q = 2a. Это геометрическое место - эллипс с фокусами Р и Q, проходящий через точку R на прямой L, причем прямая L касается этого эллипса в точке R. Действительно, если бы прямая L пересекала эллипс еще в какой-то точке, кроме R, то существовал бы отрезок прямой L, лежащий внутри эллипса; для каждой точки этого отрезка р + q было бы меньше, чем 2а: в самом деле, легко убедиться, что р + q меньше или больше, чем 2а, смотря по тому, находится ли рассматриваемая точка внутри или вне эллипса. Но так как мы знаем, что для точек на прямой L непременно р + q ≥ 2а, то сделанное предположение приходится отбросить. Итак, прямая L - касательная к эллипсу в точке R. Кроме того, мы знаем, что PR и RQ образуют одинаковые углы с L; отсюда в качестве побочного результата наших рассуждений вытекает важная теорема: касательная к эллипсу образует равные углы с прямыми, проведенными из фокусов в точку касания.

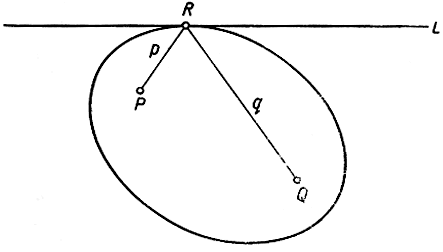
Рис. 181. Свойство касательной к эллипсу

Следующая задача родственна предыдущей. Дана прямая линия L и две точки Р и Q по разные стороны L (рис. 182); требуется найти такую точку R на L, чтобы величина |р - q|, т. е. абсолютное значение разности расстояний точки R от Р и Q, была как можно больше. (Мы допускаем, что L не является перпендикуляром, восставленным из середины отрезка РQ: иначе р - q равнялось бы нулю для всякой точки L, и задача потеряла бы смысл.) Приступая к решению задачи, построим зеркальное отражение точки Р относительно L: полученная точка Р' расположена по ту же сторону L, что и Q. Какова бы ни была точка R' на L, мы имеем: р = R'P = R'P', q = R' Q. Так как разность двух сторон треугольника никогда не превышает третьей стороны, то, рассматривая треугольник R' QP', можно заключить, что величина |р - q| = |R'P' - R'Q| меньше или равна Р'Q; и, как видно из чертежа, только при условии, что R", Р' и Q расположены на одной прямой, |р - q| может оказаться равным Р'Q. Поэтому искомая точка R есть точка пересечения прямой L с прямой, проведенной через Р' и Q. Как и в предыдущей задаче, не представляет труда установить, ссылаясь на конгруэнтность треугольников RPR' и RP'R что углы, которые с прямой L делают отрезки RP и RQ, одинаковы.

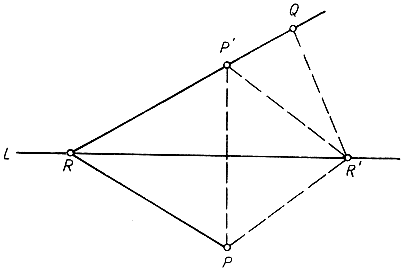
Рис. 182. |PR - QR| = maximum

Отсюда, как и в прежней задаче, уже ничего не стоит получить свойство касательной к гиперболе. Принимая наибольшее значение разности |PR - RQ| равным 2а, рассмотрим геометрическое место всех точек в плоскости, для которых абсолютное значение р - q равно 2а. Это - гипербола с фокусами Р и Q, проходящая через точку R. Легко убедиться, что абсолютное значение р - q меньше, чем 2а, в области, заключенной между двумя ветвями гиперболы, и больше, чем 2а, по ту сторону каждой из ветвей, по которую лежит соответствующий фокус. Отсюда - в основном с помощью такой же аргументации, как и в случае эллипса,- вытекает, что прямая L касается гиперболы в точке R. К которой именно из ветвей прямая L является касательной,- это зависит от того, которая из точек Р и Q ближе к L: если ближе точка Р, то касается прямой L та ветвь, которая окружает Р; и аналогично для Q (рис. 183). Если Р и Q находятся на равных расстояниях от прямой L, то L не касается ни той, ни другой ветви гиперболы, а является одной из ее асимптот. Об этом результате позволительно догадываться, исходя из того соображения, что описанное выше построение в рассматриваемом случае не дает никакой (конечной) точки P, так как прямая P'Q оказывается параллельной прямой L.

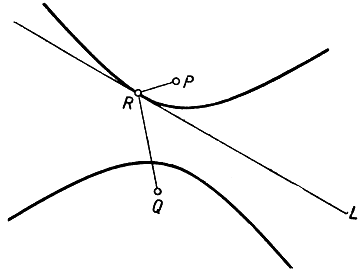
Рис. 183. Свойство касательной к гиперболе

Так же, как и в случае эллипса, наши рассуждения приводят к хорошо известной теореме: касательная, проведенная в любой точке гиперболы, делит пополам угол между отрезками, проведенными из фокусов в точку касания.

Может показаться странным, что приходится решать задачу о минимуме, если точки Р и Q лежат по одну сторону L, тогда как, если точки лежат по разные стороны L, мы рассматриваем задачу о максимуме. Но нетрудно прийти к заключению, что указанное различие совершенно естественно. В первой задаче при удалении по прямой L в бесконечность - в одну или в другую сторону - каждое из расстояний р и qб следовательно и их сумма, неограниченно возрастает. Таким образом, было бы невозможно найти наибольшее значение р + q, и единственной возможной является постановка задачи о минимуме. Дело обстоит совершенно иначе во второй задаче, когда Р и Q лежат по разные стороны L. В этом случае не будем смешивать три различные величины: разность р - q, обратную разность q - р и абсолютное значение |р - q|; именно для последней величины мы определяли максимум. Как обстоит дело, легче всего понять, если представить себе, что точка R движется по прямой L, занимая различные положения R₁, R₂, R₃, ... . Существует такое положение R, для которого разность р - q обращается в нуль; при этом прямая L пересекается с перпендикуляром к отрезку PQ, проведенным из его середины. Ясно, что при этом положении точка R дает минимум для абсолютного значения р - q. Но по одну сторону от этой точки р больше, чем q, по другую - меньше; значит, величина р - q положительна по одну сторону точки и отрицательна - по другую. Следовательно, сама эта величина не имеет ни максимума, ни минимума в точке, где |р - q| = 0. С другой стороны, та точка, в которой |р - q| имеет максимум, наверное, дает экстремум для р - q. Если р>q, то имеется максимум для р - q; если q>р, то максимум для q - р и, значит, минимум для p - q. Имеется ли максимум или минимум для р - q, это зависит от положения двух данных точек относительно прямой L.

В случае, если Р и Q находятся на равных расстояниях от L, решения задачи о максимуме, как мы видели, нет вовсе, так как прямая Р'Q (см. рис. 182) параллельна L. И тогда при удалении R в бесконечность в том или в другом направлении величина |р - q| стремится к некоторому конечному пределу. Этот предел есть не что иное, как длина s проекции отрезка РQ на прямую L (читатель может доказать это в качестве упражнения). Величина |р - q| при рассматриваемых обстоятельствах всегда меньше, чем предел s, и максимума не существует, так как, какова бы ни была данная точка R, всегда можно указать другую, более удаленную, для которой |р - q| будет больше и, однако, еще не совсем равно s.