3. Применения к задачам о треугольниках

С помощью теоремы Герона можно легко решить следующие две задачи.

а) Задана заранее площадь А и одна сторона с = PQ треугольника; среди всех такого рода треугольников требуется найти тот, для которого сумма двух других сторон а и b наименьшая. Вместо того чтобы задавать сторону с и площадь А треугольника, можно задать сторону с и высоту h, опущенную на с, так как 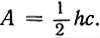Таким образом, задача сводится к тому, чтобы найти точку R (рис. 180), находящуюся на расстоянии h от прямой PQ, и притом такую, что сумма сторон а + b обращается в минимум. Из первого условия следует, что точка R должна быть расположена на прямой, параллельной прямой PQ и отстоящей от нее на расстоянии h. Раз это установлено, становится ясно, что задача решается с помощью теоремы Герона в применении к тому случаю, когда Р и Q находятся на одном и том же расстоянии от прямой L: искомый треугольник PRQ равнобедренный.

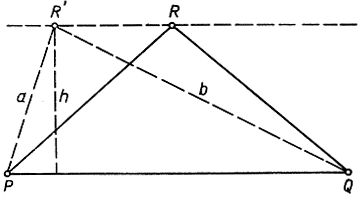
Рис. 180. Треугольник наименьшего периметра при данных основании и площади

b) В треугольнике пусть даны: одна сторона с и сумма а + b двух других сторон; требуется из всех таких треугольников выбрать тот, у которого площадь наибольшая. Эта задача - обратная по отношению к задаче а). Решением является опять-таки равнобедренный треугольник, для которого а = b. Как мы уже видели, для такого треугольника при заданной площади сумма а + b принимает наименьшее значение; это значит, что во всяком другом треугольнике с основанием с и той же площадью сумма а + b имеет большее значение. С другой стороны, из а) ясно, что во всяком треугольнике с основанием с и площадью, большей, чем площадь рассматриваемого равнобедренного треугольника, значение а + b также будет больше. Отсюда следует, что всякий другой треугольник, имеющий заданные значения для а + b и для с, должен иметь меньшую площадь, так что наибольшую площадь при заданных с и а + b имеет именно равнобедренный треугольник.