2. Теорема Герона. Экстремальное свойство световых лучей

Экстремальное свойство световых лучей Дана прямая L и две точки Р и Q по одну и ту же ее сторону. Как выбрать точку R на прямой L с таким расчетом, чтобы сумма отрезков PR + RQ давала кратчайший путь от Р к Q с заходом на L? В этом заключается проблема Герона о световом луче (точно такую же проблему приходится решать тому, кто, желая из точки Р как можно скорее пройти в точку Q, должен был бы по дороге подойти к L: представьте себе, что L - берег реки, и там нужно зачерпнуть ведро воды). Чтобы получить решение, построим зеркальное отражение Р' точки Р относительно прямой L, и тогда прямая Р' Q пересекает L как раз в искомой точке R. Легко доказать, что PR + RQ меньше, чем PR' + R'Q, где R' - любая точка на L, отличная от R.

Действительно, PR = P'R и PR' = = P'R' значит, PR + RQ = P'R + + RQ - P'Q и PR' + R'Q = P'R' + R'Q. Ho P'R' + R'Q больше, чем P'Q (так как сумма двух сторон треугольника больше третьей стороны), т. е. PR' + R'Q больше, чем PR + RQ, что и требовалось доказать. В дальнейшем существенно предполагать, что Р и Q не лежат на самой прямой L.

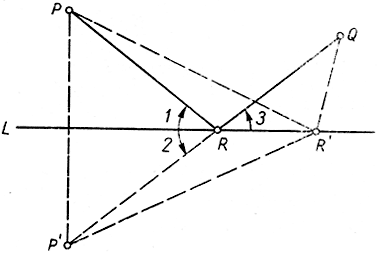
Рис. 177. Теорема Герона

Из рис. 177 видно, что ∠3 = ∠2 и ∠2 = ∠1, так что ∠1 = ∠3. Другими словами, точка R такова, что PR и QR образуют одинаковые углы с L. Отсюда следует, что световой луч, отражающийся от L (а при отражении, как показывает эксперимент, угол падения равен углу отражения), действительно обращает в минимум путь из Р в Q с заходом на L - в согласии с высказанным утверждением.

Задачу можно обобщить, вводя несколько прямых L, М, ... . Рассмотрим, например, случай, когда имеются две прямые L, М и две точки Р, Q, расположенные, как на рис. 178, и поставим целью найти кратчайший путь из Р в Q с заходом сначала на L, потом на М. Пусть Q' - отражение Q относительно М и Q" - отражение Q' относительно L. Проведем прямую PQ", пересекающую L в точке R, и прямую RQ", пересекающую М в точке S; тогда PR + RS + SQ и есть искомый кратчайший путь. Доказательство подобно приведенному выше и предоставляется читателю в качестве упражнения. Если бы L и М были зеркалами, то световой луч из Р, приходящий после отражения в L, потом в М в точку Q, попадал бы на L в точке R, а на М - в точке S; итак, световой луч опять-таки избрал бы для себя путь наименьшей длины.

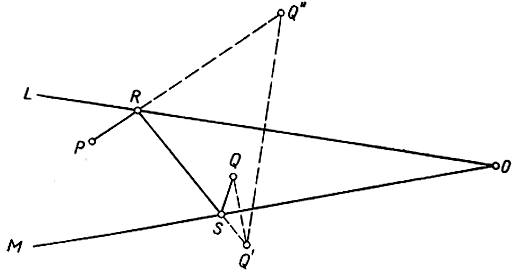
Рис. 178. Отражение в двух зеркалах

Можно было бы также поставить задачу нахождения кратчайшего пути из Р в Q с заходом сначала на М, потом на L. Таким должен быть путь PRSQ (рис. 179), определяемый аналогично пути PRSQ, рассмотренному раньше. Длина этого нового пути может оказаться или большей, или меньшей, или равной длине прежнего пути.

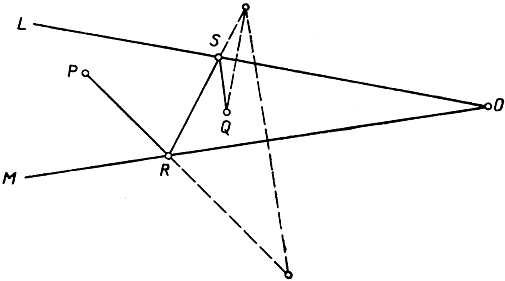
Рис. 179. Вариант предыдущей задачи

^*Упражнение. Показать, что новый путь больше прежнего в том случае, если точки Q и R лежат по одну сторону прямой РQ. В каком случае новый и прежний пути окажутся равными?