§ 1. Задачи из области элементарной геометрии

1. Треугольник наибольшей площади при двух заданных сторонах

Даны два отрезка а и b требуется найти треугольник возможно большей площади, у которого две стороны были бы а и b. Решением является прямоугольный треугольник с катетами а и b. Рассмотрим в самом деле какой-нибудь треугольник с двумя сторонами а и b (рис. 176). Если h есть высота, соответствующая основанию а, то площадь треугольника А равна 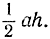Это последнее выражение, очевидно, принимает наибольшее значение при наибольшем возможном значении h, что случится именно при h, равном b, т. е. тогда, когда треугольник прямоугольный. Итак, максимальная площадь равна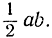

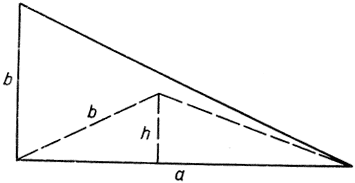
Рис. 176. Максимум площади треугольника при двух данных сторонах