
*5. Пределы при итерации
Нередко приходится рассматривать последовательности, сконструированные таким образом, что аn+1 получается из аn посредством тех же операций, посредством каких аn получается из аn+1: эта процедура позволяет вычислить любой член последовательности, если известен первый. В подобных случаях говорят о процедуре "итерации".
Примером может служить последовательность
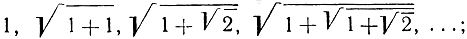
каждый член ее получается из предыдущего посредством прибавления единицы и затем извлечения квадратного корня. Таким образом, последовательность определяется соотношениями
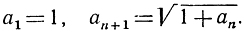
Найдем ее предел. Очевидно, что при n>1 и аn>1. Далее, последовательность наша монотонно возрастает, так как
a2n+1 - a2n = (1 + an) - (1 + an-1) = an - an-1.
Раз только аn>аn-1, то значит, аn+1>аn; но a2 - a1 = √2 - 1 > 0, и потому (с помощью индукции) отсюда следует, что аn+1>аn; при всех значениях n. Мы замечаем дальше, что рассматриваемая последовательность ограниченная; в самом деле,
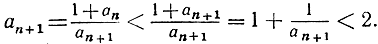
В силу принципа монотонных последовательностей отсюда вытекает существование предела: аn→а, причем 1<a≤2. Но видно ясно, что а есть положительный корень уравнения х2 = 1 + х: действительно, соотношение а2n+1 = 1 + аn в пределе при n→∞ дает нам аn = 1 + а. Решая уравнение, мы убеждаемся, что 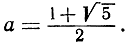
Отсюда, наоборот, легко сделать тот вывод, что это квадратное уравнение можно решать приближенно, с какой угодно степенью точности, посредством итерационной процедуры.
Таким же образом, с помощью итераций, можно решать и другие алгебраические уравнения. Например, кубическое уравнение х3 - 3x + 1 = 0 напишем в форме
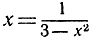
и затем, взяв в качестве а1 произвольное число, скажем а1 = 0, определим дальше последовательность аn по формуле
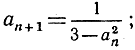
при этом получим
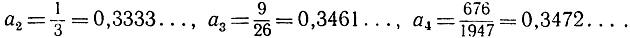
Можно показать, что последовательность имеет предел, равный корню данного кубического уравнения, а именно а = 0,3473... .
Итерационные процессы в этом роде имеют громадное значение в математике, так как с их помощью большей частью даются "доказательства существования"; они полезны и в приложениях, где доставляют методы приближенного решения разнообразных проблем.
Упражнения на пределы. При n→∞:
- Докажите, что
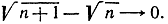 (Указание. Напишите разность в виде
(Указание. Напишите разность в виде
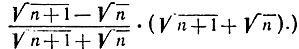
- Найдите предел
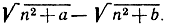
- Найдите предел
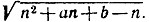
- Найдите предел
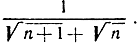
- Докажите, что предел
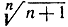 равен 1.
равен 1.
- Каков предел
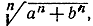 если а>b>0?
если а>b>0?
- Каков предел
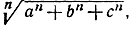 если а>b>с>0?
если а>b>с>0?
- Каков предел
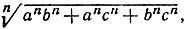 если а>b>с>0?
если а>b>с>0?
- Мы увидим позднее, что
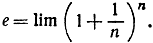 Используя это, найти предел
Используя это, найти предел 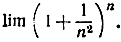
|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'