4. Разрывные функции как предел непрерывных

Будем рассматривать такие последовательности а_n, в которых члены а_n не постоянные числа, а функции некоторой переменной х, именно а_n = f_n(x). Если только такая последовательность сходящаяся, то ее предел также есть функция х:

Такого рода представления функции f(x) в виде предела других функций часто бывают полезны, так как "более сложные" функции таким образом приводятся к "более простым".

В частности, это обнаруживается при рассмотрении некоторых явных формул, определяющих функции с разрывами. Рассмотрим, например, последовательность 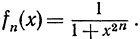При |х| = 1 мы получаем 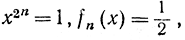так что 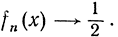С другой стороны, при |x|<1 мы имеем х²ⁿ→0 и f_n(x)→1; наконец, при х>1 получается х²ⁿ→∞ и, следовательно, f_n (x)→0. В итоге

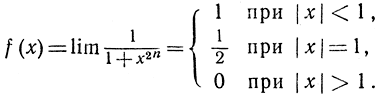
Мы видим, что прерывная функция f(x) представлена как предел последовательности непрерывных рациональных функций.

Другой интересный пример в таком же роде дается последовательностью

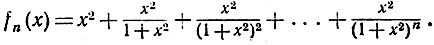
При х = 0 все функции f_n(x) обращаются в нуль, и потому f(0) = lim f_n(0) = 0. При х≠0 выражение 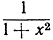положительно и меньше, чем 1, и потому теория геометрической прогрессии позволяет утверждать, что f_n(x) сходится при n→∞. Предел, т. е. сумма бесконечной прогрессии, равен 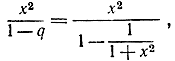Итак, f_n(x) стремится к функции f(x) = 1 + x² при х ≠0 и к f(x) = 0 при х = 0. Получается функция f(x) с устранимым разрывом в точке х = 0.