
3. Предел n√p
Последовательность чисел
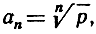
т. е.
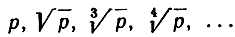
имеет предел 1, каково бы ни было положительное число р:
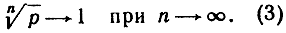
(3)
(Символ 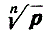 обозначает, как всегда, положительный корень степени n. В случае, если р отрицательно, при n четном не существует действительных корней степени n.)
обозначает, как всегда, положительный корень степени n. В случае, если р отрицательно, при n четном не существует действительных корней степени n.)
Докажем соотношение (3). Предположим, прежде всего, что р>1; тогда также √p>1. Мы можем положить
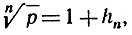
причем hn - положительная величина, зависящая от n. Из неравенства (2) следует
p = (1 + hn)n>nhn.
Деление на n дает
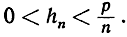
Так как последовательности bn = 0 и 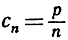 обе имеют предел 0, то на основании рассуждения, приведенного в пункте 1, hn также при возрастании n имеет предел 0, и наше утверждение, таким образом, доказано в случае р>1. Мы встретились здесь с очень типическим примером, когда предельное соотношение, в данном случае hn→0, устанавливается посредством заключения hn между двумя границами, пределы которых определяются более просто.
обе имеют предел 0, то на основании рассуждения, приведенного в пункте 1, hn также при возрастании n имеет предел 0, и наше утверждение, таким образом, доказано в случае р>1. Мы встретились здесь с очень типическим примером, когда предельное соотношение, в данном случае hn→0, устанавливается посредством заключения hn между двумя границами, пределы которых определяются более просто.
Кстати, мы получили оценку для разности hn между 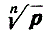 и 1: эта разность непременно меньше, чем
и 1: эта разность непременно меньше, чем 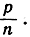
Если 0<р<1, то 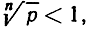 и можно положить
и можно положить
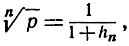
где hn - снова положительное число, зависящее от n. Отсюда следует
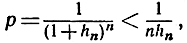
так что
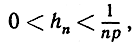
и, значит, hn стремится к нулю при n→∞. И тогда, очевидно, 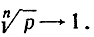 "Уравнивающее" воздействие извлечения корня степени n, выражающееся в том, что результаты извлечения корней последовательно возрастающих степеней из данного положительного числа приближаются к единице, остается в силе иногда и в том случае, если само подрадикальное выражение не остается постоянным. Мы проверим сейчас, что
"Уравнивающее" воздействие извлечения корня степени n, выражающееся в том, что результаты извлечения корней последовательно возрастающих степеней из данного положительного числа приближаются к единице, остается в силе иногда и в том случае, если само подрадикальное выражение не остается постоянным. Мы проверим сейчас, что
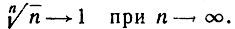
Небольшое ухищрение позволит нам сослаться опять на неравенство (2). Вместо корня степени n из n возьмем корень степени n из √n. Полагая 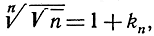 где kn - положительная величина, зависящая от n, получим с помощью упомянутого неравенства √n = (1 + kn)n>nkn, так что
где kn - положительная величина, зависящая от n, получим с помощью упомянутого неравенства √n = (1 + kn)n>nkn, так что
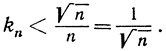
Значит,
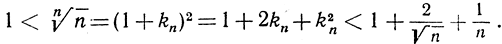
Правая часть этого неравенства стремится к 1 при n→∞, и потому то же самое можно сказать относительно 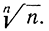
|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'