2. Предел q^n

Если q - число, большее, чем 1, то члены последовательности qⁿ неограниченно возрастают; например, так будет при q = 2:

Такие последовательности "стремятся к бесконечности" (см. стр. 325). В самом общем случае доказательство этого основывается на важном неравенстве (см. стр. 39):

где h - какое угодно положительное число. Мы положим q = 1 + h, где h>0; тогда

Пусть k - сколь угодно большое положительное число; в таком случае достаточно взять 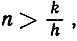чтобы получить неравенство

значит, qⁿ→∞. Если q = 1, то все члены последовательности равны 1 и, значит, предел последовательности есть 1. Если q отрицательно, то знаки qⁿ чередуются, и в случае |q|≥ 1 предела нет.

Упражнение. Дайте строгое доказательство последнему утверждению.

На стр. 90 мы установили, что если -1<q<1, то qⁿ→0. Дадим здесь еще другое, очень простое доказательство. Рассмотрим случай 0<q<1. Тогда члены последовательности q, q², q³, ... монотонно убывают, оставаясь положительными. Отсюда следует (см. стр. 328), что последовательность имеет предел: qⁿ→a. Умножая обе части последнего соотношения на q, получим: qⁿ⁺¹→aq.

Но qⁿ⁺¹ должно иметь тот же предел, что и qⁿ, так как дело не меняется от того, как обозначен возрастающий показатель - через n или через n+1. Значит, aq = а, или a(q - 1) = 0. Так как по условию 1-q ≠ 0, то отсюда следует а = 0.

Если q = 0, предыдущее утверждение тривиально. Если, наконец, -1<q<0, то 0<|q|<1; поэтому, как только что доказано, |qⁿ| = |q|ⁿ→0. Но в таком случае qⁿ→0 при условии |q|<1. Доказательство закончено.

Упражнения. Доказать, что при n→∞

1. 
2. 
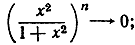
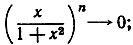
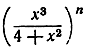3. стремится к бесконечности при x>2, к нулю при |x|<2.