§ 6. Некоторые применения теоремы Больцано

1. Геометрические применения

С помощью простой и общей теоремы Больцано можно доказать некоторые утверждения, на первый взгляд отнюдь не представляющиеся вполне очевидными. Установим, прежде всего, следующее: Если А и В - две заданные фигуры на плоскости, то существует такая прямая в этой плоскости, которая обе фигуры одновременно делит на равновеликие (в смысле площади) части. Под "фигурой" здесь понимается всякая часть плоскости, ограниченная простой замкнутой кривой.

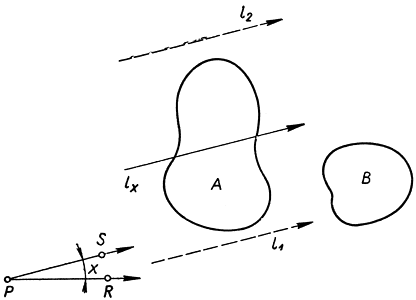
Рис. 173. Одновременное деление пополам двух площадей

Начнем доказательство с того, что выберем произвольную фиксированную точку Р в нашей плоскости и проведем из нее фиксированный луч PR, от которого будем вести отсчет углов. Каков бы ни был луч PSб делающий угол х с лучом PR, существует направленная прямая, параллельная PS и делящая фигуру А на равновеликие части. Действительно, возьмем одну из направленных прямых, параллельных PS и имеющих всю фигуру А по одну сторону: пусть эта прямая будет l₁; станем подвергать ее параллельному перенесению таким образом, чтобы при окончательном положении (которое назовем l₂) вся фигура А оказалась уже по другую ее сторону (рис. 173). В таком случае функция, определяемая как разность площади части А, расположенной вправо от направленной прямой, и площади части A, расположенной влево ("вправо" - "к востоку", "влево" - "к западу", если прямая направлена, скажем, "на север"), оказывается положительной для положения прямой l₁ и отрицательной для положения l₂. Так как эта функция непрерывна, то. по теореме Больцано, она обращается в нуль при каком-то промежуточном положении прямой, которое мы обозначим теперь через l_x и при котором, очевидно, фигура А разбивается пополам. Итак, каково бы ни было х (0°≤х<360°) существует прямая l_x, разбивающая А пополам.

Обозначим теперь через y = f(x) разность между площадью части фигуры В справа от l_x и площадью части В слева от l_x. Допустим для определенности, что прямая l₀, параллельная PR и разбивающая А пополам, справа имеет большую часть площади В, чем слева; тогда y положительно при х = 0°. Пусть теперь х возрастает до 180°: тогда прямая l₁₈₀, параллельная RP и разбивающая А пополам, совпадает с l₀ (но направлена в противоположную сторону, а "правая" и "левая" стороны переместились); отсюда ясно, что значение y при х = 180° численно то же, что и при х = 0°, но с обратным знаком, т. е. отрицательно. Так как у есть функция х, непрерывная при 0°≤х≤180° (упомянутая разность площадей, очевидно, изменяется непрерывно при вращении секущей прямой), то существует такое значение х = α, при котором y обращается в нуль. Но тогда прямая l_α разбивает пополам обе фигуры А и В одновременно. Наша теорема доказана.

Следует заметить, что мы установили всего-навсего существование прямой, обладающей заданным свойством, но не указали определенной процедуры для ее построения: в этом - характерная черта "чистых" математических доказательств существования.

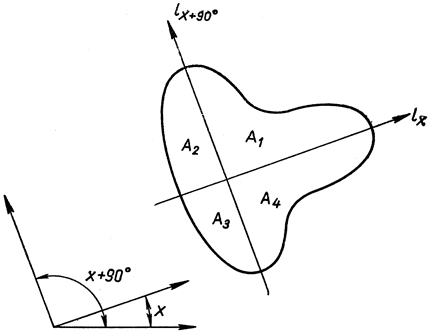
Рис. 174. Деление площади на четыре равные части

Вот другая, аналогичная проблема: дана одна фигура А на плоскости; требуется разбить ее на четыре равновеликие части двумя взаимно перпендикулярными прямыми. Чтобы доказать существование решения, вернемся к тому этапу решения предыдущей проблемы, когда была введена прямая l_x, но фигура В еще не была введена в рассуждение. Рассмотрим прямую l_х+90, перпендикулярную к l_x и также разбивающую A пополам. Если занумеруем четыре части A так, как показано на рис. 174, то получим, очевидно,

и

Отсюда вычитанием получим

т. е.

а значит,

Итак, существование решения нашей проблемы будет доказано, если установим существование такого угла α, что для прямой l_α будет удовлетворено равенство двух частей нашей фигуры

так как отсюда будет вытекать равенство всех четырех частей. Рассмотрим теперь функцию y = f(x),

где А₁ (х) и А₂ (х) - части фигуры, соответствующие прямой l_x. При х = 0° пусть будет, например, f(0) = A₁ (0) - A₂ (0)>0. Тогда при х = 90° получится: f(90) = A₁ (90) - A₂ (90) = A₂ (0) - A₃ (0) = A₂ (0) - A₁ (0)<0. Но f(х) - непрерывная функция; значит, при каком-то значении а между 0 и 90° получится f(α) = A₁ (α) - A₂ (α) = 0. Тогда прямые l_α и l_α+90° разбивают фигуру на четыре равновеликие части.

Эти проблемы обобщаются на случай трех и большего числа измерений. В случае трех измерений первая проблема формулируется следующим образом: даны три пространственных тела; требуется найти плоскость, разбивающую каждое из них пополам одновременно. Доказательство возможности решения также основывается на теореме Больцано. В случае большего числа измерений аналогичное утверждение также справедливо, но доказательство требует применения более тонких методов.