*4. Одна теорема о последовательностях. Компактные множества

Пусть х₁, х₂, х₃, ... есть некоторая бесконечная последовательность чисел, различных или нет, содержащихся в отрезке I: a≤x≤b. Последовательность может стремиться или не стремиться к пределу. Но как бы то ни было, всегда можно извлечь из такой последовательности, выбрасывая некоторые из ее членов, такую новую бесконечную последовательность y₁, y₂, y₃, ..., которая стремилась бы к пределу, заключенному в отрезке I.

Чтобы доказать эту теорему, разделим интервал I с помощью средней точки 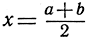на два отрезка I' и I":

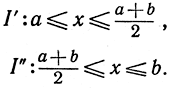
По крайней мере в одном из них будет находиться бесчисленное количество членов х_n основной последовательности: обозначим его через I₁. Выберем один из этих членов х_n1 и обозначим его через y₁. Проделаем то же самое с отрезком I₁. Так как на отрезке I₁ имеется бесконечное множество членов х_n, то их должно быть бесконечное множество также и по крайней мере в одной из половин I₁; обозначим эту половину через I₂. На отрезке I₂ возьмем член х_n, для которого n>n₁, и обозначим его через y₂. Продолжая таким же образом, мы можем найти последовательность вложенных отрезков I₁, I₂, I₃, ... и подпоследовательность y₁, y₂, y₃, ... членов основной последовательности таким образом, что y_n лежит на отрезке I_n, каково бы ни было n. Эта последовательность отрезков стягивается к некоторой точке у промежутка, и ясно, что последовательность y₁, y₂, y₃, ... имеет предел y, что и требовалось доказать.

^* Эти рассуждения допускают обобщение того типа, который характерен для современной математики. Рассмотрим переменное X, пробегающее некоторое множество S, в котором каким-то образом определено понятие "расстояния". S может быть множеством точек на плоскости или в пространстве. Но это не является необходимым; например, S может быть также множеством всех треугольников на плоскости. Если Х и Y являются двумя треугольниками с вершинами А, В, С и А', В', С' соответственно, то в качестве "расстояния" между треугольниками можно взять, например, число

где АА' обозначает обычное расстояние между точками А и А', и т. д. Как только во множестве введено понятие "расстояния", мы имеем возможность определить понятие последовательности элементов X₁, Х₂, Х₃, ..., стремящейся к пределу X - также элементу множества S. Мы подразумеваем под этим, что d (X, Х_n)→0 при n→∞. Теперь мы скажем, что множество S компактно, если из каждой последовательности Х₁, Х₂, Х₃, ... элементов этого множества можно извлечь подпоследовательность, стремящуюся к некоторому пределу X, принадлежащему множеству S. В предыдущем пункте мы показали, что замкнутый отрезок а≤х≤b компактен в указанном смысле. Таким образом, понятие компактного множества можно считать обобщением понятия замкнутого отрезка на числовой оси. Отметим, что числовая ось в целом некомпактна, поскольку последовательность целых чисел 1, 2, 3, 4, 5, ... не стремится ни к какому пределу и не содержит в себе никакой подпоследовательности, которая бы стремилась к пределу. Также и открытый интервал некомпактен, например, 0<x<1, не включающий конечных точек; действительно, последовательность 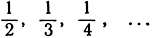или любая ее подпоследовательность стремится к пределу 0, который не принадлежит, однако, рассматриваемому открытому промежутку. Таким же образом можно показать, что область плоскости, состоящая, скажем, из внутренних точек некоторого квадрата или прямоугольника, некомпактна; но она становится компактной после присоединения точек границы. Нетрудно также убедиться, что множество всех треугольников с вершинами, лежащими внутри или на окружности данного круга, компактно.

Понятие непрерывности допускает обобщение на случай, когда переменное X пробегает любое множество S, лишь бы в этом последнем было предварительно введено понятие стремления к пределу. Говорят, что функция u = F (X) (где и мыслится как действительное число) непрерывна на элементе X, если всякий раз, как последовательность элементов Х₁, Х₂, Х₃, ... имеет предел X, соответствующая последовательность чисел F (X₁), F (X₂), F (Х₃), ... имеет предел F (X). (Можно дать определение и с помощью ε, δ) Легко также убедиться, что теорема Вейерштрасса остается в силе для случая обобщенной непрерывной функции F (X), заданной на некотором компактном множестве:

Если u = F (X) есть непрерывная функция, определенная для всех элементов компактного множества S, то существует обязательно такой элемент S, для которого F (X) достигает своего наибольшего значения, и другой элемент, для которого F (X) достигает своего наименьшего значения.

Доказательство не представит никакого труда для того, кто схватил общий характер относящихся сюда идей; мы не пойдем дальше в этом же направлении. Мы увидим в главе VIII, что теорема Вейерштрасса в ее общей формулировке имеет особенно большое значение в теории максимумов и минимумов.