3. Теорема Вейерштрасса об экстремальных значениях

Другой существенный и интуитивно ясный факт, касающийся непрерывных функций, был сформулирован Карлом Вейерштрассом (1815-1897), который, возможно, более чем кто бы то ни было другой, является ответственным за современное стремление к строгости в математическом анализе. Эта теорема утверждает: Если функция f(x) непрерывна в интервале I, а≤х≤b, не исключая также и конечных точек интервала а и b, то в интервале I должна существовать по крайней мере одна точка, в которой функция f(x) достигает своего наибольшего значения М, и другая точка, в которой функция f(x) достигает своего наименьшего значения m. Говоря интуитивно, это значит, что график непрерывной функции u = f(x) должен иметь по крайней мере одну наивысшую и одну наинизшую точки.

Существенно отметить, что это утверждение может быть неверным, если функция f(x) перестает быть непрерывной в конечных точках промежутка I. Например, функция f(x) = 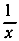не имеет наибольшего значения в промежутке 0<х≤1, хотя она и непрерывна внутри промежутка. И вместе с тем разрывная функция вовсе не обязательно достигает наибольшего и наименьшего значений, даже если она ограничена. Рассмотрим, например, "чрезвычайно" разрывную функцию f(x), определенную следующим образом:

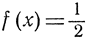при рациональном х,

в промежутке 0≤x≤1. Все значения, которые принимает эта функция, заключены между 0 и 1. Среди них имеются сколь угодно близкие к 0 и 1: они получаются, если х будем выбирать иррациональным и достаточно близким к 0 или 1. Но f(x) никогда не может быть равным ни 0, ни 1, поскольку для рациональных х мы имеем 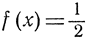, а для иррациональных мы имеем f(x) = х. Итак, значения 0 и 1 ни в какой точке не достигаются.

^* Теорема Вейерштрасса может быть доказана почти таким же образом, как и теорема Больцано. Разобьем интервал I на два замкнутых полуинтервала I' и I" и фиксируем наше внимание на I', как на интервале, в котором следует искать наибольшее значение функции f(х), если только в интервале I" не найдется такой точки α, что f(α) больше всех значений функции f (x) в интервале I'; в этом последнем случае мы выберем интервал I". Тот интервал, который мы выбрали, обозначим через I₁. Поступим теперь с интервалом I₁ точно так же, как мы поступали с I; пусть при этом получим интервал I₂ и т. д. Этот процесс определит последовательность I₁, I₂, ..., I_n, ... вложенных интервалов, которые все содержат некоторую точку z. Мы докажем, что значение функции в этой точке f(z) = М есть наибольшее из всех значений функции f(х), достигаемых в исходном интервале, т. е. что не может существовать такой точки s, что f(s)> М. Предположим, что нашлась бы точка s, удовлетворяющая условию f (s) = = М + 2ε, где ε есть некоторое (может быть, и очень маленькое) положительное число. В силу непрерывности функции f(х) мы можем точку z окружить маленьким интервалом К, не захватывающим точки s, и притом таким, что в интервале К значения функции f(х) отличаются от f(z) = М меньше, чем на ε, так что в нем мы непременно будем иметь f(х)<М + ε. Но при достаточно больших n интервал I_n лежит внутри интервала К, а вместе с тем интервал I_n был определен так, что ни одно значение f(х) при х, лежащем вне интервала I_n не может превзойти значений функции f(x) в точках х из этого интервала.

Но точка s лежит вне интервала I_n и в ней f(s)> М + ε, тогда как в интервале К, а тем самым в интервале I_n мы имеем f(х)<M + ε. Таким образом, мы пришли к противоречию.

Существование по крайней мере одного наименьшего значения m может быть доказано тем же самым методом; впрочем, оно является следствием предыдущего, так как наименьшее значение функции f(х) является наибольшим значением функции g(x) = - f(x).

Теорема Вейерштрасса может быть доказана аналогичным образом и для непрерывных функций от двух или большего числа переменных х, y, ... . В этом случае придется вместо замкнутых интервалов (со включением конечных точек) брать замкнутые области, например прямоугольники в плоскости х, y (со включением контура).

Упражнение. В каком пункте доказательств теорем Больцано и Вейерштрасса мы воспользовались предположением, что функция f(x) определена и непрерывна во всем отрезке (замкнутом) а≤х≤b, а не только при a<x≤b или а<х<b?

Доказательства теорем Больцано и Вейерштрасса носят явно неконструктивный характер. Они не предоставляют метода для "эффективного" нахождения положения нулевой точки или наибольшего и наименьшего значения функции с заранее назначенной степенью точности в результате конечного числа операций. Доказано только лишь само существование, или, вернее, абсурдность несуществования, упомянутых значений. Это обстоятельство представляет собой еще один важный пункт, против которого "интуиционисты" (см. стр. 115) выдвинули свои возражения; некоторые из них даже настаивали, чтобы подобные теоремы были вообще изгнаны из математики. Изучающий математику не должен, впрочем, принимать эти возражения более серьезно, чем это сделало большинство критиков.