*2. Доказательство теоремы Больцано

Дадим строгое доказательство этой теоремы. Если следовать Гауссу и другим великим математикам, то можно принять этот факт и без доказательства. Нашей целью является сведение этой теоремы к основным свойствам системы действительных чисел, в частности к постулату Дедекинда - Кантора о стягивающихся отрезках (стр. 95). Для этого рассмотрим отрезок I, a≤x≤b, в котором задана функция f(x), разобьем его на два средней точкой 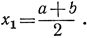Если в этой средней точке мы получим f(x₁)=0, то доказывать больше уже нечего. Если, однако, f(x₁)≠0, то f(x₁) должно быть или больше, или меньше нуля. В обоих случаях одна из половинок отрезка I будет снова обладать тем свойством, что знаки значений функции f(х) на его концах различны.

Обозначим этот отрезок через I₁. Мы повторим этот процесс, деля отрезок I₁ пополам; тогда в середине I₁ или имеем f(x) = 0, или мы можем выбрать такую половину I₂ отрезка I₁ для которой опять знаки значений функции на двух концах различны. Повторяя эту процедуру, мы, в конце концов, или найдем после конечного числа делений точку, в которой f(x) = 0, или получим последовательность стягивающихся отрезков I₁, I₂, I₃, ... . В последнем случае постулат Дедекинда-Кантора обеспечивает существование в исходном отрезке / такой точки а, которая принадлежит всем отрезкам сразу. Мы утверждаем, что f(α) = 0, так что а и будет той точкой, существование которой нужно доказать.

До сих пор предположение о непрерывности функции f(x) использовано еще не было. Сейчас придется на него сослаться, заканчивая доказательство способом от противного. Мы докажем, что f(α) = 0, допуская противоположное и приходя затем к противоречию. Предположим, что f(α) ≠ 0: пусть, например, f(α) = 2ε > 0. Так как функция f(х) непрерывна, то мы найдем (может быть, маленький) отрезок J длины 2δ с центром в точке α - такой, что значение функции f(х) во всем отрезке I отличается от f (α) меньше, чем на ε. Затем, так как f(α) = 2ε, то мы можем быть уверены, что f(х) >ε в каждой точке J, т. е. что f (х)>0 в отрезке I. Но отрезок J фиксирован, и если n достаточно велико, то маленький отрезок I_n должен непременно попасть внутрь I, поскольку последовательность длин I_n стремится к нулю. В этом заключается противоречие: в самом деле, из того, каким образом был выбран отрезок I_n, вытекает, что функция f(х) имеет противоположные знаки в двух конечных точках каждого отрезка I_n, так что функция f (х) принимает отрицательные значения где-то на отрезке J. Отсюда следует ложность предположения f(α)>0, а также (совершенно таким же образом) f(α)<0; следовательно, доказано, что f(α) = 0.