§ 5. Две основные теоремы о непрерывных функциях

1. Теорема Больцано

Бернард Больцано (1781-1848), католический священник, знаток схоластической философии, был одним из первых, кто ввел в математический анализ современное понятие строгости. Его замечательная книжка "Paradoxien des Unendlichen" появилась в 1850 г. Здесь впервые было признано, что многие, казалось бы, очевидные утверждения, касающиеся непрерывных функций, могут и должны быть доказаны, если имеется в виду применять их во всей их общности. Примером этого может служить следующая теорема о функциях одного переменного.

Непрерывная функция переменного х, положительная при некотором значении х и отрицательная при некотором другом значении х из замкнутого интервала непрерывности а≤х≤b, должна обращаться в нуль при некотором промежуточном значении х. Итак, если функция f(х) непрерывна при изменении х от а до b, и при этом f(a)<0 и f(b)>0, то существует такое значение α переменного х, что а<α<b и f(а) = 0.

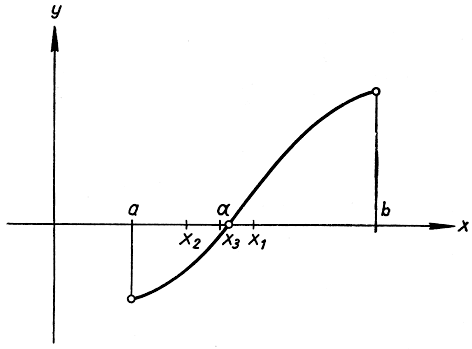
Рис. 172. Теорема Больцано

Теорема Больцано прекрасно согласуется с нашим интуитивным представлением о непрерывной кривой, которая неизбежно должна пересечь в какой-нибудь точке ось х, чтобы перейти с одной ее стороны на другую. Что, напротив, это не обязательно в случае разрывной функции, показывает рис. 157 на стр. 315.