§ 4. Точное определение непрерывности

В § 1, пункт 5, мы ввели следующее определение непрерывности функции: функция f(x) непрерывна в точке х = х₁, если при стремлении х к х₁ величина f(x) стремится к пределу, равному f(x₁). Если мы проанализируем эту формулировку, то увидим, что она подразумевает выполнение следующих двух требований:

a) существует предел а функции f(x) при стремлении переменной х к пределу x₁,

b) этот предел а должен быть равен f(x).

Если в определении предела на стр. 337 мы подставим вместо а его значение f(x₁), то условие непрерывности принимает следующий вид: функция f(x) непрерывна при х = х₁, если, как бы мало ни было положительное число ε, можно подобрать такое положительное число δ (зависящее от ε), что неравенство

будет выполнено для всех х, удовлетворяющих условию

(ограничение х≠x₁ введенное в определении предела, здесь излишне, поскольку неравенство |f(x) - f(x₁)|<ε при х = х₁ удовлетворяется автоматически).

В качестве примера постараемся установить непрерывность функции f(x) = х³, скажем, в точке х₁ = 0. Мы имеем:

Выберем теперь маленькое положительное число ε, например 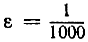. Мы должны показать, что, ограничивая значения х числами, достаточно близкими к 0, получим соответствующие значения функции f(x), отличающиеся от 0 меньше, чем на ¹/₁₀₀₀, т. е. заключенные между 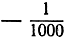и 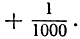Мы сразу видим, что значения f(x) не выйдут из этих границ, если мы ограничим изменение х значениями, отличающимися от 0 меньше, чем на 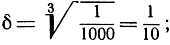в самом деле, если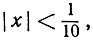
то 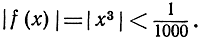Совершенно так же мы можем взять вместо 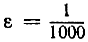меньшее значение ε = 10^-4, 10^-5 и т. д.; числа 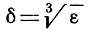будут удовлетворять нашему требованию, так как из неравенства 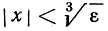следует неравенство |f(x)| = |x³|<ε.

Основываясь на определении непрерывности с помощью ε, δ, можно доказать аналогично, что все полиномы, рациональные функции и тригонометрические функции непрерывны в любой точке, за исключением, может быть, тех изолированных значений х, около которых функции становятся бесконечными.

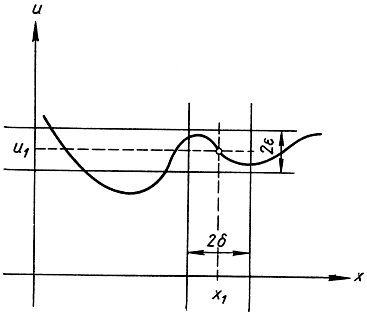
Рис. 170. Функция, непрерывная в точке х = х₁

Связывая определение непрерывности с графиком функции u = f(x), можно придать ему следующую геометрическую форму. Выберем некоторое положительное число ε и начертим прямые, параллельные оси х на высоте f(x₁) - ε и f(x₁) + ε над ней. Тогда должно найтись такое положительное число δ, что вся часть графика, лежащая внутри вертикальной полоски шириной в 2δ около x₁, содержится также и в горизонтальной полоске шириной в 2ε около f(x₁). Рис. 170 показывает функцию, непрерывную в точке x₁, в то время как рис. 171 показывает функцию, имеющую разрыв в этой точке. В последнем случае, как бы узка ни была вертикальная полоска около x₁, она всегда будет содержать часть графика, лежащую вне горизонтальной полоски шириной 2ε.

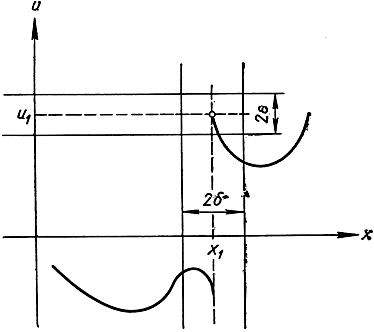
Рис. 171. Функция имеет разрыв в точке х = х₁

Если я утверждаю, что данная функция u = f(x) непрерывна в точке х = х₁, то это значит, что я беру на себя по отношению к вам следующие обязательства: вы можете выбрать любое положительное число ε, сколь угодно малое, но определенное. Тогда я обязуюсь подыскать такое положительное число δ, чтобы неравенство |x - x₁|<δ влекло за собой неравенство |f(x) - f(x₁)|<ε. Но при этом я не обязуюсь найти такое число δ, которое подошло бы ко всякому ε, которое вы назовете потом: мой выбор δ зависит от вашего выбора ε. Если вы можете выбрать хоть одно ε, для которого я не смогу подобрать подходящего δ, то моя игра проиграна - мое утверждение опровергнуто. Для того чтобы доказать, что я могу выполнить мое обязательство в конкретном случае некоторой функции u = f(x), мне нужно построить явно такую положительною функцию

определенную для всякого положительного числа ε, для которой я могу доказать, что из неравенства |х - х₁|<δ следует всегда неравенство |f(х) - f(х₁)<ε. В случае функции u = f (х) = х³ при х = 0 функцией δ = φ (ε) была .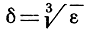

Упражнения.

1. Доказать, что sin x и cos x - функции непрерывные.
2. Доказать непрерывность функций

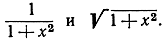
Теперь становится ясным, что определение непрерывности с помощью ε, δ не находится в противоречии с тем, что мы могли бы назвать "наблюдаемыми фактами", относящимися к функциям. Таким образом, оно соответствует основному принципу современной науки, который выдвигает в качестве критерия полезности некоторого понятия или "существования" явления (в научном смысле) возможность непосредственно его наблюдать (по крайней мере в принципе) или сводить его к фактам, доступным наблюдению.