4. Пределы при x→∞

Если непрерывная переменная х достаточно велика, то функция 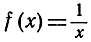становится произвольно малой, или "стремится к О". В самом деле, поведение этой функции при возрастающем х по существу то же самое, что и поведение последовательности 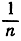при возрастании n. Мы вводим общее определение: Функция f(x) имеет предел а при х, стремящемся к бесконечности, и записываем это в форме

если, как бы мало ни было положительное число ε, можно к нему подобрать такое положительное число К (зависящее от ε), что неравенство

выполняется при условии |x|>К (сравнить с соответствующим определением на стр. 323).

В случае функции 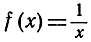, для которой а = 0, достаточно выбрать 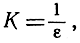в чем читатель может убедиться немедленно.

Упражнения.

1. Показать, что с точки зрения вышеприведенного определения утверждение
   f (х)→а при х→∞
   эквивалентно следующему:
   
   подсказать, что имеют место следующие предельные соотношения при хℯ∞:
   
   
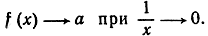
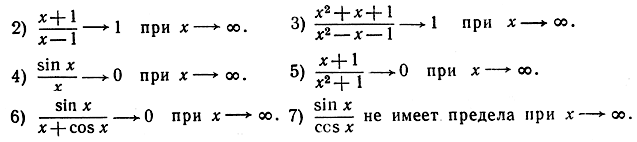
2. Дайте определение "f (x)→∞ при x→∞'". Приведите пример.

Имеется следующая разница между случаем функции f (x) и случаем последовательности а_n. В случае последовательности n может стремиться к бесконечности не иначе, как возрастая, тогда как в случае функции переменная х, неограниченно возрастая, имеет право принимать как положительные, так и отрицательные значения. Если желательно направить внимание на поведение функции f (x) только при больших положительных значениях, то условие |x|>К мы должны заменить условием х>K; напротив, для случая больших по абсолютной величине отрицательных значений х вводим условное х<-K. Чтобы символизировать эти два способа "одностороннего" стремления к бесконечности, мы пишем соответственно: