
3. Предел sin x/x
Если х обозначает угол в радианном измерении, то выражение 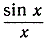 определено для всех значений х, за исключением значения х = 0, при котором оно принимает вид не имеющего смысла символа 0/0. С помощью таблиц тригонометрических функций читатель может подсчитать значение частного
определено для всех значений х, за исключением значения х = 0, при котором оно принимает вид не имеющего смысла символа 0/0. С помощью таблиц тригонометрических функций читатель может подсчитать значение частного 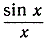 для малых значений х. Эти таблицы обычно даются для градусного измерения углов; мы напоминаем (см. § 1, пункт 2), что градусная мера х связана с радианной мерой у следующим соотношением:
для малых значений х. Эти таблицы обычно даются для градусного измерения углов; мы напоминаем (см. § 1, пункт 2), что градусная мера х связана с радианной мерой у следующим соотношением: 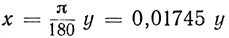 (с точностью до пятого десятичного знака). Из четырехзначных таблиц мы находим следующие значения:
(с точностью до пятого десятичного знака). Из четырехзначных таблиц мы находим следующие значения:

Хотя точность чисел здесь ограничивается четырьмя знаками, все же эти данные приводят к мысли, что
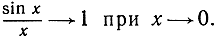
Сейчас мы дадим строгое доказательство этому предельному соотношению.
В силу определения тригонометрических функций с помощью единичного круга, мы имеем следующие соотношения для величины х, являющейся радианной мерой угла ВОС (см. рис. 169) при ограничении 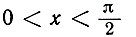 .
.
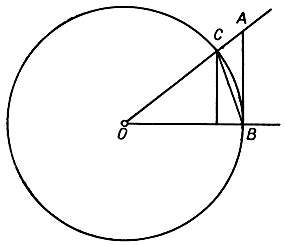
Рис. 169. Основное тригонометрическое неравенство
Площадь треугольника 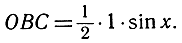
Площадь кругового сектора 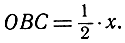
Площадь треугольника 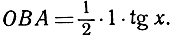
Отсюда вытекает двойное неравенство:
sin x <x< tg x
Деля на sin x, получим, далее,
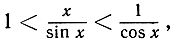
или
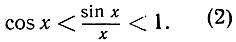
Но, с другой стороны,
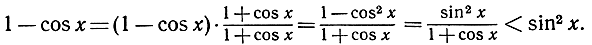
Так как sin x< x, то отсюда следует, что
1 - cos x < x1 (3)
или
1 - х2 < cos x.
Совместно с неравенством (2) это дает окончательно нужные нам неравенства
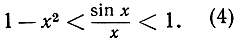
Мы предполагаем, что 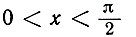 ; однако неравенства (4) справедливы и при условии
; однако неравенства (4) справедливы и при условии 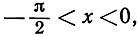 поскольку
поскольку
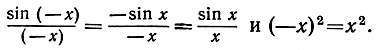
Предельное соотношение (1) вытекает немедленно из неравенств (4). В самом деле разность между 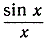 и 1 меньше, чем х2, а х2 может быть сделано меньше, чем любое число ε, если только взять |x|<δ = √ε.
и 1 меньше, чем х2, а х2 может быть сделано меньше, чем любое число ε, если только взять |x|<δ = √ε.
Упражнения.
- Вывести из неравенства (3) предельное соотношение
Найти пределы при х→0 следующих функций:
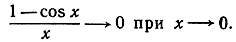 предполагая, что x измеряется в градусах,
предполагая, что x измеряется в градусах,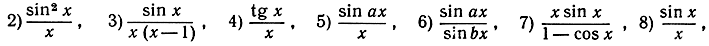
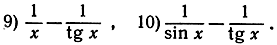
|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'