2. Замечания по поводу понятия предела

ε-δ-определение предела - результат столетних попыток и блужданий; оно кратко воплощает результат неустанных усилий поставить понятие предела на здравую математическую основу. Важнейшие понятия анализа - производная и интеграл - могут быть определены не иначе, как с помощью перехода к пределу. Но ясное понимание и строгое определение самого понятия предела долгое время казались непреодолимо трудными.

При изучении движения в частности и какого бы то ни было изменения в общем случае математики XVII и XVIII столетий принимали, как нечто достаточно наглядное и не подлежащее дальнейшему анализу, концепцию величины х, меняющейся и в своем непрерывном течении приближающейся к предельному значению х₁. Они рассматривали другую величину u = f(x), зависящую от времени или от какой-нибудь другой, зависящей от времени, величины х. Оставалось все же проблемой: какой точный математический смысл следует приписывать представлению о том, что f(х) "стремится" или "приближается" к определенному значению а, когда х движется к х₁?

Однако еще со времен Зенона и его парадоксов все попытки дать точную математическую формулировку интуитивному физическому или метафизическому понятию непрерывного движения были безуспешными. Нет затруднений в продвижении шаг за шагом по дискретной последовательности значений а₁, а₂, а₃, ... . Но когда приходится иметь дело с непрерывной переменной х, пробегающей целый интервал значений на числовой оси, то описание того, как х "приближается" к заданному значению х₁, затруднено тем, что принимаемые значения из интервала не могут быть указаны последовательно в порядке их возрастания. В самом деле, точки прямой представляют везде плотное множество, и не существует точки, "следующей" за данной. Остается неизбежное расхождение между интуитивной идеей и точным математическим языком, предназначенным для того, чтобы описывать ее основные линии в научных, логических терминах. Парадоксы Зенона ярко обнаруживают это несоответствие.

Существенным достижением Коши является то, что он ясно осознал, что, поскольку дело касается математических понятий, всякая ссылка на интуитивное представление о непрерывном движении должна быть отброшена. Как случается нередко, подлинный научный прогресс был осуществлен тогда, когда последовал отказ от попыток прибегать к метафизическим объяснениям и было принято решение вести рассуждение, оставаясь на почве строго математических понятий, соответствующих "наблюдаемым фактам" в физике. Если мы проанализируем логически, что надлежит понимать под "непрерывным приближением" и какие существуют способы для того, чтобы в каждом отдельном случае проверить, имеет ли место таковое, то мы вынуждены будем принять именно то самое определение, которое дано Коши, и никакое иное. Это определение - статическое; оно не опирается на интуитивную идею движения. Более того, только такое статическое определение позволяет подвергнуть точному математическому анализу само непрерывное движение и разрешает парадоксы Зенона по крайней мере в той их части, которая относится к математике.

В определении с помощью ε, δ независимое переменное не "движется"; оно не "стремится" и не "приближается" к пределу х₁ в каком бы то ни было физическом смысле. Правда, эти обороты речи, как и символ →, сохраняются, причем математик вовсе не обязан отказываться от тех, в общем-то весьма полезных, интуитивных представлений, которые с ними связываются. Но когда в каком-либо конкретном случае нужно дать ответ на вопрос, существует предел или не существует, то приходится прибегнуть именно к определению с помощью ε, δ. Спрашивать о том, насколько удовлетворительно это определение соответствует интуитивному "динамическому" представлению о стремлении к пределу, можно с таким же правом, как и о том, насколько удовлетворительно аксиомы геометрии описывают то, что мы называем пространством (в интуитивном смысле).

Обе формулировки в какой-то степени предоставляют возможность работать воображению, и вместе с тем обе они создают адекватную математическую основу для дальнейшего логического построения.

Как и в случае предела последовательности, ключ к правильному пониманию определения Коши лежит в обращении "естественного" порядка, в котором рассматриваются переменные. Прежде мы отмечаем границу ε для зависимого переменного, а уже потом стремимся определить подходящую границу δ для независимого переменного. Когда мы говорим, что "f(x)→a при х→х₁", то лишь сокращенно высказываем ту мысль, что этот процесс может быть выполнен для любого положительного числа ε. В частности, ни одна из частей этого утверждения, например, "x→x₁", не имеет смысла сама по себе.

Еще нужно подчеркнуть следующее. Заставляя х "стремиться" к х₁, мы можем позволить х быть больше или меньше, чем х₁, но возможность равенства явно исключается требованием х≠х₁ стремится к х₁, но никогда не принимает значения х₁. Таким образом, мы можем применять наше определение к функциям, не определенным вовсе при х = х₁, но имеющим тот или иной предел при х, стремящемся к х₁, например к функции 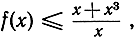рассмотренной на стр. 335. Исключение значения х = х₁ как раз соответствует тому факту, что, рассматривая последовательности а_n при n→∞ например, предел a_n = ¹/_n), мы никогда не подставляем в формулу значения n = ∞.

Однако что касается функции f(x), то, когда х стремится к х₁, ей не запрещено стремиться к пределу а таким образом, что при некоторых значениях х≠ x₁ осуществляется равенство f(x) = а. Например, рассматривая функцию 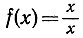при х, стремящемся к 0, мы никогда не позволяем х быть равным 0, но зато, напротив, равенство f(x) = 1 справедливо при всех х≠0, и предел а существует и равен 1 в точном согласии, с определением.