
§ 3. Пределы при непрерывном приближении
1. Введение. Общие определения
В § 2 (стр. 323) нам удалось дать точное определение утверждению: "Последовательность аn (т. е. функция аn = F(n) натурального переменного n) имеет предел а при n, стремящемся к бесконечности". Теперь мы дадим соответствующее определение утверждению: "Функция u = f(x) непрерывной переменной х имеет предел а при стремлении х к значению x1".
В интуитивной форме понятие предела при непрерывном приближении независимого переменного х употреблялось уже в § 1, пункт 5, когда нужно было установить, непрерывна ли рассматриваемая функция в данной точке.
Начнем опять с частного примера. Функция 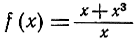 определена для всех значений x, не равных нулю; при этом последнем значении х знаменатель уничтожается. Если мы вычертим график функции y = f(x) для значений х в окрестности точки 0, то станет очевидным, что при х, "стремящемся" к 0 с любой стороны, соответствующие значения u = f(x) "стремятся" к пределу 1. Для того чтобы дать точное описание этого факта, найдем явную формулу разности между значением функции f (х) и постоянного числа 1:
определена для всех значений x, не равных нулю; при этом последнем значении х знаменатель уничтожается. Если мы вычертим график функции y = f(x) для значений х в окрестности точки 0, то станет очевидным, что при х, "стремящемся" к 0 с любой стороны, соответствующие значения u = f(x) "стремятся" к пределу 1. Для того чтобы дать точное описание этого факта, найдем явную формулу разности между значением функции f (х) и постоянного числа 1:
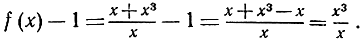
Если мы условимся рассматривать лишь значения х, близкие к 0, но не равные самому нулю (для которого функция f(x) даже не определена), мы можем разделить числитель и знаменатель на х и получить более простую формулу
f(x) - 1 = х2.
Ясно, что эту разность мы можем сделать сколь угодно малой, ограничивая изменение переменной х достаточно малой окрестностью значения х≤0. Так, например, при 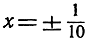 имеем
имеем 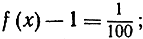 при
при 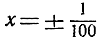 имеем
имеем 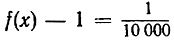 и т. д. Вообще, если е есть некоторое положительное число, то, как бы мало оно ни было, разность между f(x) и 1 будет меньше чем ε, если только расстояние точки х от точки 0 меньше числа δ = √ε.
и т. д. Вообще, если е есть некоторое положительное число, то, как бы мало оно ни было, разность между f(x) и 1 будет меньше чем ε, если только расстояние точки х от точки 0 меньше числа δ = √ε.
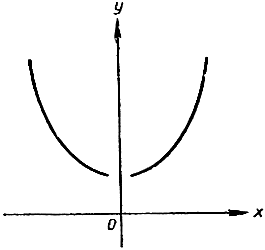 ">
">Рис. 168.
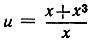
В самом деле, если |, x|<√εто
|f(x) - 1| = |x2|<ε.
Аналогия с нашим определением предела последовательности полная. На стр. 323 мы дали определение: Последовательность аn имеет предел а при n, стремящемся к бесконечности, если каждому положительному числу ε, как бы мало оно ни было, можно поставить в соответствие такое целое N (зависящее от ε), что неравенство
|аn-а|<ε
выполняется для всех n, удовлетворяющих неравенству
n≥N.
В случае функции f(x) непрерывного переменного х при х, стремящемся к некоторому конечному значению х1, мы просто слова "достаточно большое n" (что характеризуется числом N) заменяем словами "достаточно близко к х1" (что характеризуется числом δ) и приходим к следующему определению предела при непрерывном приближении, впервые данному Коши около 1820 г.: Функция f(x) имеет предел а, когда х стремится к значению x1, если для каждого положительного (сколь угодно малого) числа ε найдется такое положительное число δ (зависящее от ε), что
|f(x) - а|<ε
для всех значений х≠x1, удовлетворяющих неравенству
|х - х1|<δ.
Если это имеет место, принято писать:
f (х)→а при х→x1.
В случае функции 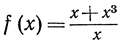 мы выше показали, что эта функция f(x) имеет предел 1 при х, стремящемся к значению х1 = 0. В этом случае достаточно было всегда выбирать δ = √ε.
мы выше показали, что эта функция f(x) имеет предел 1 при х, стремящемся к значению х1 = 0. В этом случае достаточно было всегда выбирать δ = √ε.
|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'