
*5. Непрерывные дроби
Интересные бесконечные процессы возникают в связи с непрерывными дробями. Конечная непрерывная дробь, такая, как
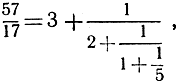
представляет собой некоторое рациональное число. На стр. 74 мы показали, что каждое рациональное число может быть выражено в такой форме с помощью алгорифма Евклида. Однако в случае иррациональных чисел алгорифм не заканчивается после конечного числа операций. Напротив, он ведет к последовательности все более" "длинных" дробей, из которых каждая представляет собой рациональное число. В частности, все действительные алгебраические числа (см. стр. 131) степени 2 могут быть выражены таким образом. Рассмотрим, например, число x = √2 -1 являющееся корнем квадратного уравнения
х2 + 2х = 1,
или
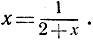
Если в правой части заменить х снова дробью 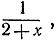 то это дает выражение
то это дает выражение
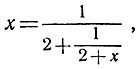
а затем
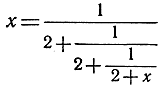
и т. д., так что после n "шагов" получим равенство
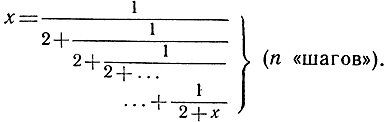
Если n стремится к бесконечности, мы получим "бесконечную непрерывную дробь"
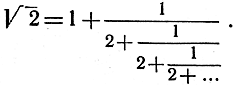
Эта замечательная формула связывает число √2 с целыми числами гораздо более удивительным образом, чем это делает десятичное разложение √2, которое не обнаруживает никакой правильности в чередовании десятичных знаков.
Для положительного корня любого квадратного уравнения вида
х2 = ах + 1,
или
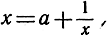
мы получаем разложение
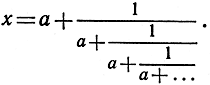
Например, полагая а = 1, мы находим
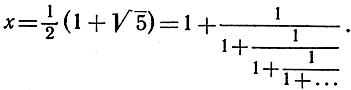
Эти примеры являются частными случаями общей теоремы, утверждающей, что действительные корни квадратного уравнения с целыми коэффициентами разлагаются в периодическую непрерывную дробь, подобно тому как рациональные числа разлагаются в периодические десятичные дроби.
Эйлер сумел найти почти столь же простые разложения в непрерывные дроби для чисел е и π. Приведем их без доказательств:
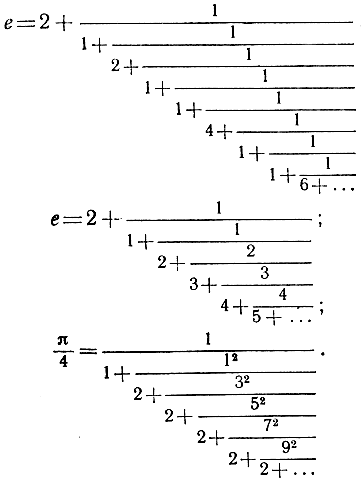
|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'