4. Число π

Как известно из школьной математики, длина окружности, радиус которой равен единице, может быть определена как предел последовательности длин периметров правильных многоугольников при бесконечном увеличении числа их сторон. Определенная таким образом длина окружности обозначается символом 2π. Точнее, если через р_n обозначить длину вписанного, а через q_n длину описанного правильного n-угольника, то имеют место неравенства

Более того, когда n возрастает, обе последовательности р_n и q_n приближаются монотонно к 2π, и на каждом этапе мы получаем все меньшую ошибку в том приближении, которое р_n и q_n дают для числа 2π.

На стр. 153 мы получили выражение

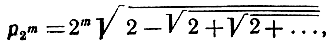
содержащее m-1 квадратных корней. Эту формулу можно использовать для подсчета приближенного значения числа 2π.

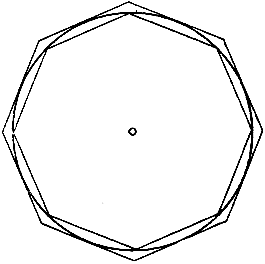
Рис. 167. Приближение окружности многоугольниками

Упражнения.

1. Найти приближенное значение π, даваемое числами р₄, p₈ и p₁₆.
2. ^* Найти формулу для q_2m.
3. ^* С помощью этой формулы вычислить q₄, q₈ и q₁₆. Зная величины р₁₆ и q₁₆, установить границы, между которыми должно лежать число π.

Что же это за число π? Неравенство р_n<2π<q_n дает на это полный ответ при развертывании последовательности вложенных интервалов, которые стягиваются к точке 2π. И все же этот ответ оставляет желать еще чего-то, поскольку он ничего не говорит о природе я как действительного числа: является ли оно рациональным или иррациональным, алгебраическим или трансцендентным? Как мы уже указывали на стр. 135, число я есть число трансцендентное, а следовательно, иррациональное. В противоположность доказательству для е доказательство иррациональности π, впервые данное Ламбертом (1728-1777), в достаточной мере трудно и здесь приведено не будет. Однако ряд сведений о числе π мы можем сообщить. Имея в виду, что целые числа являются существенной основой математики, мы можем задать вопрос: связывается ли число π сколько-нибудь просто и непосредственно с целыми числами? Десятичное разложение числа π, хотя и вычисленное с несколькими сотнями знаков, не обнаруживает ни малейшей закономерности. Это и не удивительно: ведь π и число 10 не имеют между собой ничего общего. Однако Эйлер (XVIII в.) и другие нашли изящные выражения, связывающие число я с целыми числами с помощью бесконечных рядов и произведений. Простейшей из таких формул является, вероятно, следующая:

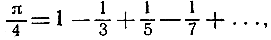
выражающая 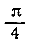как предел при возрастающем n сумм

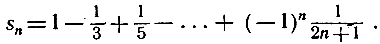
Эту формулу мы выведем в главе VIII. Вот другой бесконечный ряд, который может служить для вычисления π:

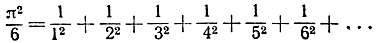
И еще одно удивительное выражение для π было открыто английским математиком Джоном Уоллисом (1616-1703). Его формула утверждает следующее:

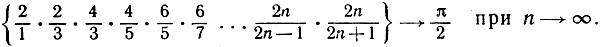
В сокращенном виде она часто записывается так:

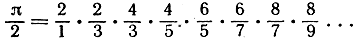
(выражения, подобные стоящему в правой части, называются бесконечными произведениями).

Доказательство последних двух формул можно найти в любом достаточно полном курсе анализа.