3. Эйлерово число е

Число е заняло видное место в математике рядом с архимедовым числом π сразу после опубликования Эйлером в 1748 г. сочинения "Introductio in Analysin Infinitorum". Это число доставит нам прекрасную иллюстрацию того, как принцип монотонных последовательностей может служить для определения нового действительного числа. Пользуясь обычной сокращенной записью для произведения n первых целых чисел

рассмотрим последовательность a₁, a₂, а₃, ..., где

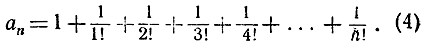
Члены последовательности а_n монотонно возрастают, поскольку а_n+1 получается из а_n посредством прибавления положительного слагаемого 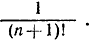Кроме того, значения а_n ограничены сверху

В самом деле, мы имеем

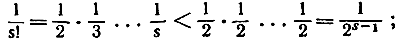
отсюда вытекает, что

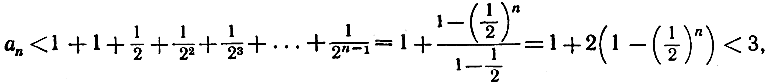
причем мы использовали формулу стр. 91 для суммы n первых членов геометрической прогрессии. Но в таком случае в силу принципа монотонных последовательностей а_n должно стремиться к некоторому пределу при стремлении n к бесконечности; этот предел обозначается буквойе. Чтобы выразить тот факт, что е = lim a_n, мы можем записать е в виде "бесконечного ряда"

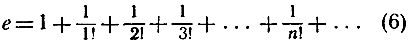
(6)

Это "тождество" с рядом точек на конце есть просто другой способ для выражения двух следующих утверждений:

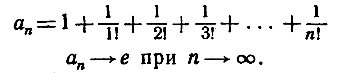
Ряд (6) позволяет вычислить е с любой степенью точности. Например, сумма (с девятью цифрами) членов ряда (6) до 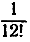включительно равна числу

(Проверьте!) "Ошибка", т. е. разность между этим приближенным и истинным значением е, может быть легко оценена. Для разности е - ∑ мы имеем выражение:

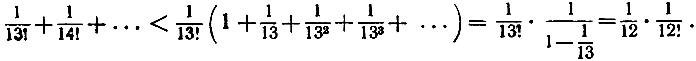
Это число так мало, что не может повлиять на девятую цифру, и потому, допуская возможную ошибку в последней цифре вышеприведенного значения, мы получаем для е следующее приближенное равенство с восемью верными цифрами:

^*Число е иррационально. Чтобы это доказать, предположим противное: допуская,

что 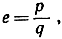где р и q - целые числа, и затем приходя к противоречию, мы должны будем заключить о нелепости сделанного предположения. Поскольку мы знаем, что 2>е>3, е не может быть целым числом, а потому q по меньшей мере должно быть равно 2. Умножим обе части тождества (6) на q! = 1*2*3...q; получим:

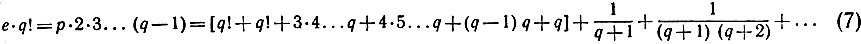
В левой части мы, очевидно, имеем целое число. В правой части слагаемое в квадратных скобках также есть целое число. Остаток же в правой части есть положительное число, меньшее ¹/₂, и, значит, не есть целое число. В самом деле, q≥2, а следовательно, члены ряда 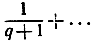не превышают соответственно членов геометрической прогрессии 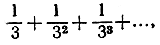сумма которых равна 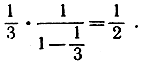Таким образом, формула (7) противоречива: целое число в левой части не может быть равно числу в правой части,

так как это последнее, являясь суммой целого числа и положительного числа, меньшего ¹/₃, не есть целое число.