2. Монотонные последовательности

В общем определении сходимости и предела на стр. 323 не содержится требований, так или иначе стесняющих характер приближения сходящейся последовательности аъ а2, а3, ... к своему пределу а. Простейший тип приближения осуществляется так называемыми монотонными последовательностями, примером которых может служить следующая:

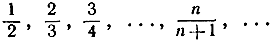
Каждый член этой последовательности больше предыдущего. Действительно,

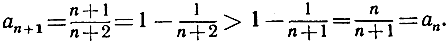
Последовательность такого рода, в которой а_n+1>а_n, называется монотонно возрастающей. Аналогично последовательность, для которой а_n>а_n+1, например, такая, как 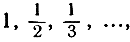называется монотонно убывающей. Последовательности этих двух типов могут приближаться к своему пределу лишь с одной стороны: "слева" или "справа". В противоположность этому существуют последовательности "колеблющиеся", например 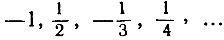Эта последовательность приближается к своему пределу 0 "с обеих сторон" (см. рис. 11, стр. 96).

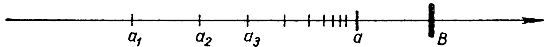
Рис. 166. Монотонная ограниченная последовательность

Монотонные последовательности обладают особенно простыми свойствами. Такого рода последовательность может не иметь предела и возрастать неограниченно, подобно последовательности

где а_n = n, или последовательности

для которой а_n есть n-е простое число р_n. В этом случае последовательность стремится к бесконечности. Но если члены монотонно возрастающей последовательности остаются ограниченными, т. е. если каждый член меньше некоторой верхней границы В, заранее известной, то интуитивно ясно, что последовательность должна стремиться к некоторому определенному пределу а, не превышающему числа В. Мы сформулируем это положение как принцип монотонных последовательностей: Монотонно возрастающая последовательность, ограниченная сверху, сходится к некоторому пределу. (Аналогичное утверждение имеет место относительно монотонно убывающей последовательности, ограниченной снизу.) Замечательно то, что значение предела а не должно быть известным заранее; теорема утверждает, что при выполнении указанных условий предел существует. Конечно, эта теорема справедлива лишь при условии, что предварительно введены иррациональные числа, и в противном случае не всегда бы оправдывалась: в самом деле, в главе II мы видели, что каждое иррациональное число (например, √2) является пределом монотонно возрастающей и ограниченной последовательности рациональных десятичных дробей, возникающих при обрывании некоторой бесконечной десятичной дроби на n-й цифре.

^* Хотя принцип монотонных последовательностей интуитивно вполне очевиден и выглядит как абсолютная истина, однако не мешает, и даже весьма полезно, привести его вполне строгое доказательство в современном стиле. Чтобы это сделать, надо показать, что этот принцип есть логический вывод из определения действительного числа и определения предела.

Предположим, что числа а₁, а₂, а₃, ... образуют монотонно возрастающую, но ограниченную последовательность. Мы можем представить члены этой последовательности как бесконечные десятичные дроби

где A_i - целые числа, а р_i, q_i, r_i и т. д.- цифры от 0 до 9. Пробежим теперь вниз по столбцу целых чисел А₁, А₂, А₃, ... Так как последовательность a₁, a₂, а₃, ... ограниченна, то эти целые числа не могут возрастать бесконечно, а поскольку она монотонно возрастает, то целые числа последовательности А₁, А₂, А₃, ... после достижения некоторого максимального значения должны стать постоянными. Обозначим это максимальное значение символом А и предположим, что оно достигнуто в N-й строке. Станем теперь пробегать второй столбец р₁, q₁, r₁ ..., сосредоточивая свое внимание на членах N₀-й и последующих строк. Если х₁ есть наибольшая из цифр, появившаяся в этом столбце после N₀-й строки, то эта цифра будет появляться всегда после своего первого появления, которое, предположим, произошло в N₁-й строке, где N₁≥N₀. (Если бы цифра в этом столбце уменьшилась когда-либо впоследствии, то последовательность а₀, а₁, а₂, ... не была бы монотонно возрастающей.) Затем мы рассмотрим цифры р₂, q₂, r₂, ... третьего столбца. Рассуждение, подобное предыдущему, показывает, что, начиная с некоторого целого числа N₂≥N₁ цифры третьего столбца постоянно равны некоторому числу х₂. Если мы повторим этот процесс для 4-го, 5-го, ... столбцов, то получим цифры x₃, x₄, х₅, ... и соответствующие целые числа N₃, N₄, N₅, ... Легко убедиться, что число

есть предел последовательности а₁, а₂, а₃, ... . В самом деле, пусть выбрано ε≥ 10^-m; тогда для всех n≥N_n целая часть и первые m цифр после запятой в числах а_n и а будут совпадать между собой, так что разность |а_n - а| не может превышать 10^-m. Так как это можно сделать для любого ε, как бы мало оно ни было, с помощью выбора достаточно большого m, то теорема доказана.

Эту теорему можно также доказать, основываясь на любом из данных в главе II определений действительного числа, например, взяв определение с помощью вложенных отрезков или дедекиндовых сечений. Такие доказательства можно найти в любом курсе анализа.

Принцип монотонных последовательностей мог бы быть применен в главе II при определении суммы и произведения двух положительных бесконечных десятичных дробей:

Два таких выражения не могут быть ни сложены, ни перемножены обычным путем, начиная с правого конца, поскольку нет никакого правого конца. ( В качестве примера читатель может попытаться сложить следующие две бесконечные десятичные дроби: 0,333333... и 0,989898... .) Но если символ х_n обозначает конечную десятичную дробь, .полученную в результате сложения конечных десятичных дробей, возникающих при "обрывании" на n-й цифре десятичных разложений а и b, то последовательность х₁, x₂, х₃, ... будет монотонно возрастающей и ограниченной (границей может служить, например, число А + В + 2). Отсюда следует, что последовательность х₁, х₂, х₃... имеет предел, и мы можем принять следующее определение:

Посредством подобного же процесса можно определить и произведение ab. Определения эти можно распространить и на все случаи, когда а и b - какие угодно положительные или отрицательные числа, применяя обычные правила арифметики"

Упражнение. Доказать, что суммой двух вышеуказанных бесконечных десятичных дробей является действительное число

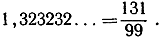
Важность понятия предела в математике заключается в том, что многие числа могут быть определены лишь как пределы (часто как пределы монотонно возрастающих последовательностей). Вот почему поле рациональных чисел, в котором такие пределы могут не существовать, слишком узко для надобностей математики.