§ 2. Пределы

1. Предел последовательности аn

Определение непрерывности функции, как мы это уже видели в § 1, основывается на понятии предела. До сих пор мы пользовались этим понятием в более или менее интуитивной форме. В настоящем и в последующих разделах мы введем его более систематическим путем. Поскольку последовательности несколько проще, чем функции непрерывного переменного, мы начнем с изучения последовательностей.

В главе II мы имели дело с числовыми последовательностями а_n и изучали их пределы при условии, что n неограниченно увеличивается или "стремится" к бесконечности. Например, последовательность с общим членом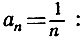

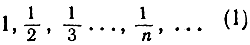
(1)

при неограниченном возрастании n имеет предел 0:

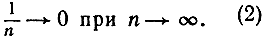
(2)

Постараемся выразить точно, что под этим подразумевается. При продвижении по последовательности все дальше и дальше мы видим, что члены становятся все меньше и меньше. После 100-го члена члены уже меньше 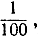после 1000-го - меньше 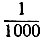и т. д. Ни один из членов не равен в действительности 0. Но если мы продвинемся достаточно далеко по последовательности (1), то мы можем быть уверены, что каждый из ее членов будет отличаться от 0 сколь угодно мало.

В этом объяснении может смущать единственно то, что смысл подчеркнутых слов не вполне ясен. Что значит "достаточно далеко" и что значит "сколь угодно мало"? Если мы сумеем придать точный смысл этим выражениям, то этим самым будет установлен точный смысл понятия предела последовательности.

Геометрическая интерпретация поможет нам разобраться в интересующем нас вопросе. Если мы изобразим члены последовательности (1)в виде соответствующих им точек на числовой оси, то заметим, что члены последовательности в нашем примере "накапливаются" или "сгущаются" около точки 0. Выберем на числовой оси некоторый интервал I с центром в точке 0 и общей длиной 2ε, так чтобы интервал простирался на расстояние ε с каждой стороны от точки 0. Если мы возьмем ε = 10, то, конечно, все члены 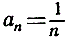нашей последовательности будут лежать внутри интервала I. Если же мы возьмем 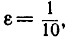то несколько первых членов окажутся лежащими вне интервала I; однако все члены, начиная с а₁₁, а именно

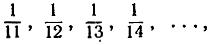
будут лежать внутри I. Даже при 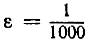лишь первая тысяча членов последовательности не попадет внутрь интервала I, тогда как бесконечное множество членов, начиная с а₁₀₀₁,

окажется внутри него. Ясно, что это рассуждение~справедливо для любого положительно числа ε: если положительное ε выбрано, то независимо от того, как оно мало, мы всегда можем подобрать настолько большое целое число N, что

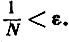
Отсюда следует, что все члены а_n последовательности, для которых n≥N, будут лежать внутри интервала I, и только конечное число членов а₁, а₂, ..., a_N-1 может лежать вне его. Основные моменты здесь таковы: во-первых, длина интервала I определяется произвольно посредством выбора ε. Затем может быть подобрано подходящее целое число N. Этот процесс первоначального выбора числа е и последующего подбора целого числа N может быть осуществлен при любом положительном ε независимо от его малости; тем самым устанавливается точный смысл утверждения, что "все члены последовательности (1) отличаются от 0 сколь угодно мало, если только мы достаточно далеко продвинемся по последовательности".

Подведем итоги: пусть ε - какое-нибудь положительное число. Тогда мы можем подобрать такое целое положительное число N, что все члены а_n последовательности (1), для которых n≥N, будут лежать внутри интервала I длины 2ε с центром в точке ε. Таков смысл предельного соотношения (2).

Опираясь на этот пример, мы можем теперь дать точное определение следующего общего утверждения: "Последовательность действительных чисел а₁, а₂, а₃, ... имеет предел а". Число а мы заключаем внутрь некоторого интервала I числовой оси: если этот интервал мал, то некоторые числа а_n могут лежать вне этого интервала, но как только n становится достаточно большим, скажем, большим или равным некоторому числу N, то все числа а_n, для которых n≥N, должны лежать внутри интервала I. Конечно, может случиться, что придется брать очень большое целое число N, если интервал I выбран очень малым; однако, как бы мал этот интервал I ни был, такое целое число N должно существовать, раз предполагается, что последовательность имеет предел.

Тот факт, что последовательность а_n имеет предел а, выражается символически следующей записью:

или просто

или

("предел а_n равен а", или "а_n стремится к пределу а"). Если последовательность имеет предел в указанном смысле, она называется сходящейся. Определение сходимости последовательности а_n можно сформулировать более сжато, а именно следующим образом:

Последовательность а₁, а₂, а₃, ... имеет предел а при неограниченном возрастании n, если каждому сколь угодно малому положительному числу ε можно поставить в соответствие такое целое положительное число N (зависящее от ε), что неравенство

выполняется для всех значений

Такова общая, "абстрактная" формулировка понятия предела последовательности. Не мудрено, если тот, кто встречается с ней впервые, не может сразу охватить и исчерпать ее содержание. К несчастью, авторы некоторых руководств, стоящие на позиции, граничащей со снобизмом, преподносят читателю это определение без тщательной подготовки, как будто снизойти до разъяснений ниже достоинства математика.

Определение предполагает своего рода дискуссию между двумя лицами А и В. A выдвигает требование: заданная величина а должна быть приближена числами а_n так, чтобы ошибка не превышала границы ε = ε₁. В отвечает на это требование указанием, что существует такое целое N = N₁,, что все члены а_n, следующие за а_N1, удовлетворяют этому условию. Тогда А становится более требовательным и предлагает новую, меньшую границу ε = ε₂; В снова встречает это требование подбором некоторого, может быть значительно большего, целого числа N = N₂, обладающего аналогичным свойством, и т. д. Если В может удовлетворить А независимо от того, какую малую границу назначает A, то мы имеем дело с положением, которое кратко выражается соотношением: а_n→а.

Имеется определенная психологическая трудность в том, чтобы составить правильное представление о понятии предела. Наша интуиция предполагает "динамическую" идею предела как результат процесса "движения": мы продвигаемся по ряду целых чисел 1, 2, 3, ..., n, ... и при этом наблюдаем за поведением последовательности а_n. Мы ждем, что числа а_n должны все меньше и меньше отличаться от числа а. Но эта "естественная" точка зрения не поддается ясной математической формулировке. Чтобы прийти к точному определению, надо обратить ход рассуждения: вместо того чтобы прежде всего обращаться к независимому переменному n_n, а затем уже к переменному а_n, мы должны основывать наше определение на том, что следует делать, если мы по существу хотим проконтролировать утверждение а_n→а. При такой постановке вопроса мы прежде всего должны выбрать произвольно малый интервал около а и затем решить: можем ли мы добиться, чтобы а_n с помощью выбора достаточно большого n в него попало. Затем, вводя символы ε и N для обозначения "произвольно малого интервала" и "достаточно большого n", мы приходим к точному определению предела.

Обращаясь теперь к другому примеру, рассмотрим последовательность

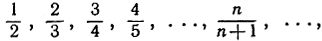
где 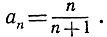Я утверждаю, что lim а_n = 1. Если вы выберете интервал с центром в точке 1 и возьмете 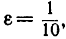то я смогу удовлетворить вашему требованию (3), выбрав N = 10; в самом деле,

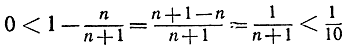
при n≥10. Если вы усилите ваше требование, выбирая 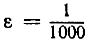, то я снова могу ему удовлетворить, выбирая N = 1000, и так далее - для любого положительного числа ε, которое вы пожелаете выбрать независимо от его малости: действительно, мне только нужно будет выбрать любое целое N, большее чем 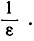Этот процесс, заключающийся, во-первых, в выборе произвольно малого интервала длины 2ε вокруг числа а и, во-вторых, в доказательстве того, что все члены последовательности а_n находятся на расстоянии, меньшем чем ε от а, раз только мы продвинемся достаточно далеко по последовательности, и есть не что иное, как подробное описание того факта, что а_n→а. Если члены последовательности а₁, а₂, а₃, ... представлены в виде бесконечных десятичных дробей, то утверждение

обозначает попросту то, что для любого целого положительного m первые m цифр числа а_n совпадают с первыми m цифрами бесконечного десятичного разложения числа а, раз только n выбрано достаточно большим, скажем, большим некоторого значения N (зависящего от m). Это просто соответствует выбору ε в форме 10^-m.

Существует другое, и очень выразительное определение понятия предела. Если lim а_n = а и если мы заключим число а в интервал I, то независимо от малости интервала I все числа а_n при n, большем некоторого целого числа N, будут лежать в интервале I, так что не больше чем конечное число N-1 членов из числа следующих:

могут лежать вне интервала I. Если интервал I очень мал, то число N может быть очень большим, скажем, равным 100 или даже 1000 биллионам, и все же лишь конечное число членов последовательности будет лежать вне интервала I, в то время как бесконечное множество оставшихся членов попадет в интервал I. Можно условиться говорить о членах некоторой бесконечной последовательности, что "почти все" они обладают некоторым свойством, если лишь конечное число их (неважно, как оно будет велико) не обладает этим свойством. Так, например, "почти все" целые положительные числа больше 1 000 000 000 000. Используя эту терминологию, мы видим, что утверждение

эквивалентно следующему утверждению: Если I есть любой интервал с центром в точке а, то почти все числа а_n лежат в этом интервале.

Не мешает мимоходом отметить, что нет необходимости предполагать, что все члены а_n последовательности непременно имеют различные значения. В частности, совершенно допустимо, чтобы несколько из них, или бесконечное число, или даже, наконец, все числа а_n были равны предельному значению а. Например, вполне законно рассматривать последовательность а₁ = 0, а₂ = 0, ..., а_n = 0, ..., и ее предел есть, конечно, 0.

Как уже указано, последовательность а_n с пределом а называется сходящейся. Последовательность, не имеющая предела, называется расходящейся.

Упражнения. Доказать:

1. Последовательность с общим числом 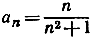имеет предел, равный 0. (Указание. 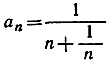меньше 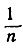и больше 0).
2. Последовательность 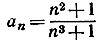имеет предел 0. (Указание: 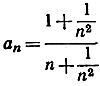лежит между 0 и ²/_n.
3. Последовательность 1, 2, 3, 4, ..., а также "колеблющиеся" последовательности
   1, 2, 1, 2, 1, 2, ...
   -1, 1, -1, 1, -1, 1, ... (т. е. а_n = (-1)ⁿ)
   и
   
   не имеют пределов.

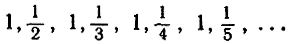
Если в последовательности а_n члены возрастают таким образом, что рано или поздно становятся больше любого наперед назначенного числа К, то принято говорить, что а_n стремится к бесконечности, и тогда пишут: lim а_n →∞, или а_n→∞. Например, n²→∞ и 2ⁿ→∞. Эта терминология удобна, хотя и не вполне последовательна, так как символ со не принято рассматривать как число. Последовательность, стремящаяся к бесконечности, считается расходящейся.

Упражнение. Докажите, что последовательность 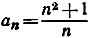стремится к бесконечности; аналогично в случае

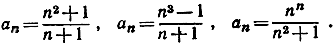
Начинающие часто впадают в ошибку, думая, что переход к пределу при n→∞ может быть выполнен совершенно просто путем подстановки n = ∞ в выражение общего члена а_n. Например, 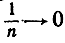потому, что 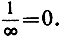Но символ ∞ не является числом, и его употребление в выражении 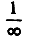незаконно. Попытка представить себе предел последовательности как "последний" член последовательности а_n при n = ∞ не попадает в цель и затемняет правильное понимание существа дела.