*7. Функции и преобразования

Соответствие между точками некоторой прямой l, характеризуемыми координатой х на этой прямой, и точками некоторой другой прямой l', характеризуемыми координатой х', есть не что иное, как некоторая функция х' = f(x). В случае взаимно однозначного соответствия имеем также и обратную функцию х = g(x'). Простейшим примером является проективное преобразование, которое задается в самом общем случае дробной линейной функцией вида

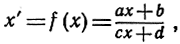
где a, b, c, d - постоянные (мы это утверждаем здесь без доказательства).

В этом примере обратная функция имеет вид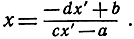

В случае, если устанавливается отображение плоскости π с координатной системой х, y на другую плоскость π' с координатной системой х', y', соотношение между точками не может быть задано одной функцией х' = f(x); здесь приходится иметь дело с двумя функциями двух переменных

Например, проективное преобразование задается системой функций

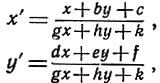
где а, b, ..., k - постоянные, а х, y и х', y', как сказано,- соответственные координаты в двух плоскостях. Теперь идея обратного отображения снова приобретает смысл. Мы просто должны решить данную систему уравнений относительно х и y, выразив их через х' и y'. Геометрически это сводится к осуществлению обратного отображения плоскости π' на плоскость π. Это отображение будет однозначно определено, если соответствие между точками обеих плоскостей взаимно однозначное.

Преобразования плоскости, изучаемые в топологии, задаются не только алгебраическими уравнениями, но вообще произвольной системой двух функций

при условии, чтобы ими определялось взаимно однозначное и взаимно непрерывное преобразование.

Упражнения

1. ^* Показать, что преобразование инверсии (глава III, стр. 172-173) в единичном круге аналитически задается уравнениями 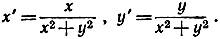Найти обратное преобразование. Доказать аналитически, что путем инверсии совокупность прямых и окружностей преобразуется в совокупность опять-таки прямых и окружностей.
2. Доказать, что преобразование 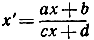четверка точек на оси х переводится в четверку точек на оси х с тем же двойным отношением (см. стр. 272.)