*6. Функции нескольких переменных

Вернемся к систематическому рассмотрению понятия функции. Если независимым переменным Р является точка плоскости с координатами х, y и если каждой такой точке Р соответствует единственное число и (например, и может быть расстоянием точки Р от начала), тогда принято писать

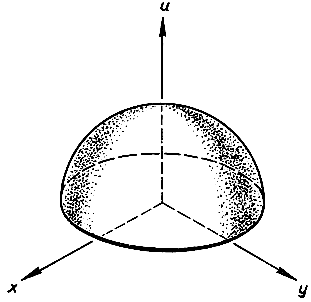
Рис. 159. Полусфера

Это обозначение употребляется также и в том случае, если, как это часто бывает, две величины х и y явно указываются самими условиями задачи как независимые переменные. Например, давление и газа есть функция объема х и температуры y, площадь и треугольника есть функция u = f(x, y, z) длин трех его сторон х, y, z.

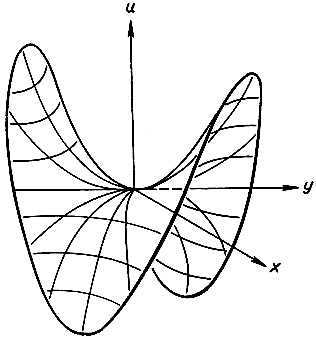
Рис. 160. Гиперболический параболоид

Так же, как график дает геометрическое представление функции одного переменного, можно получить и геометрическое представление функции u = f(x, y) двух переменных в виде поверхности в трехмерном пространстве с переменными х, y, u в качестве координат. Каждой точке х, y в плоскости x, y мы сопоставляем точку пространства с координатами х, y и u = f(x, y). Таким образом, 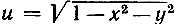представляется поверхностью сферы с уравнением u² + х² + y² = 1, линейная функция u = ах + by + с - плоскостью, функция u = ху - гиперболическим параболоидом и т. д.

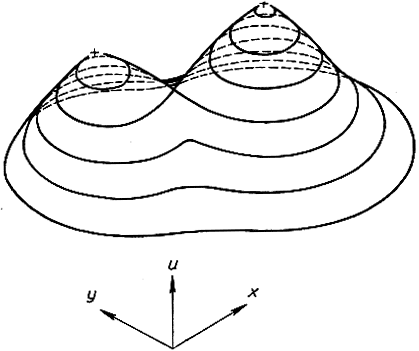
Рис. 161. Поверхность вида u = f(x, y)

Можно дать и другое представление функции u = f(x, y), притом не выходя за пределы плоскости х, y, именно с помощью линий уровня (горизонталей). Вместо того чтобы рассматривать трехмерный "ландшафт" поверхности u = f(x, y) в трехмерном пространстве, мы вычерчиваем, как это иногда делают на географических картах, "линии уровня" функции, являющиеся проекциями на плоскость х, y всех точек поверхности, находящихся на одном и том же расстоянии и по вертикали от плоскости x, y. Эти линии уровня имеют уравнения вида f(x, y) = с, где с постоянно для каждой кривой. Так, например, функция u = х + y характеризуется рис. 163. Линии уровня поверхности сферы представляют собой семейство концентрических окружностей. Функция u = х² + y², которой соответствует параболоид вращения, характеризуется также окружностями (рис. 165). Числами, отнесенными к каждой кривой, можно указывать высоту u = с.

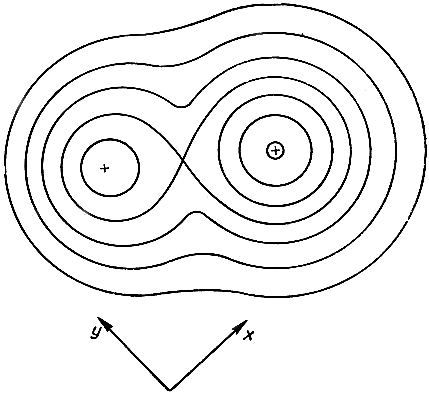
Рис. 162. Линии уровня поверхности, изображенной на рис. 161

Функции нескольких переменных встречаются в физике при описании движения непрерывной среды или каких угодно протяженных объектов. Рассмотрим хотя бы струну, натянутую между двумя точками на оси х и затем деформированную таким образом, что частица с координатой х отодвинута на некоторое определенное расстояние перпендикулярно к оси. Если струна будет отпущена, то она придет в движение, т. е. начнет колебаться; тогда точка (частица) струны с начальной координатой х в момент времени t будет находиться на расстоянии u = f(x, t) от оси х. Движение струны будет полностью определено, если только будет известна функция u = f(x, t).

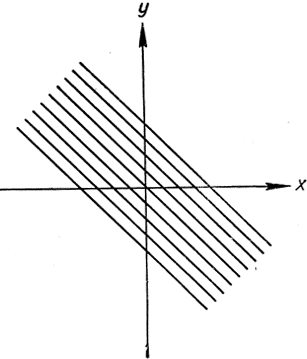
Рис. 163. Линии уровня поверхности u = x + y

Определение непрерывности, данное для функций одного переменного, распространяется непосредственно и на функции нескольких переменных. Говорят, что функция u = f(x, y) непрерывна в точке х = х₁, y = y₁, если значение f(х, y) всегда стремится к значению f(x₁, y₁), когда точка х, y приближается к точке х₁, y₁ по любому направлению или любым способом.

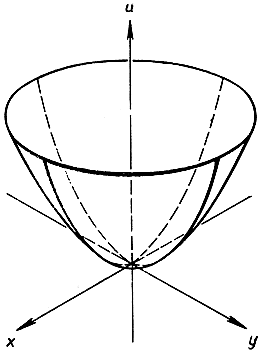
Рис. 164. Параболоид вращения

Впрочем, имеется одно существенное различие между функциями одного и нескольких переменных. В последнем случае понятие обратной функции теряет смысл, так как мы не можем решить уравнение u = f(x, y), например u = х + y, так, чтобы каждое из независимых переменных х и y было бы выражено с помощью только одного переменного u. Но это различие между функциями если мы перейдем, далее, к рассмотрению преобразований или отображений.

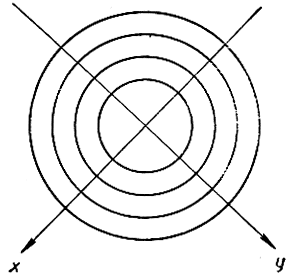
Рис. 165. Соответствующие линии уровня