5. Непрерывность

Графики уже рассмотренных функций дают интуитивное представление о свойстве, называемом непрерывностью. Точное определение этого понятия мы дадим в § 4, после того как понятие предела будет поставлено на строго логический фундамент. Здесь же, ограничиваясь описательной формулировкой, мы скажем, что функция непрерывна, если ее график есть плавная, нигде не "прерывающаяся" кривая. Чтобы уяснить себе, является ли функция u = f(x) непрерывной в точке х = х₁, заставим независимую переменную х приближаться непрерывно справа и слева к значению х₁. При этом значения функции и = f(x) меняются, если только эта функция не является постоянной в окрестности точки х₁. Если оказывается, что значение функции f(x) неограниченно приближается к значению f(x₁) этой функции в выбранной точке х = х₁ ("стремится к пределу f(x₁)"), и притом независимо от того, приближается ли х к х₁с одной стороны или с другой, то тогда говорят, что функция f(x) непрерывна в точке х₁. Если это имеет место в каждой точке х₁ из некоторого интервала, то говорят, что функция непрерывна в этом интервале.

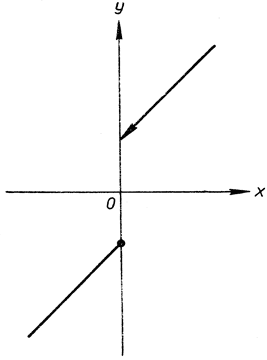
Рис. 157. Разрыв 'скачком'

Хотя каждая функция, представляемая плавным графиком, непрерывна, но очень легко определить и такие функции, которые не всюду непрерывны. Например, функция на рис. 157, определенная для всех значений х с помощью формул

разрывна в точке х₁ = 0, в которой она имеет значение -1. Если мы станем чертить карандашом график этой функции, нам придется в этой точке оторвать карандаш от бумаги. Когда мы приближаемся к значению х₁ = 0 справа, то f(x) стремится к +1. Но значение это отличается от значения функции в самой этой точке, именно -1.

Одно то обстоятельство, что функция f(x) стремится к -1, когда х стремится к нулю слева, еще недостаточно для установления непрерывности.

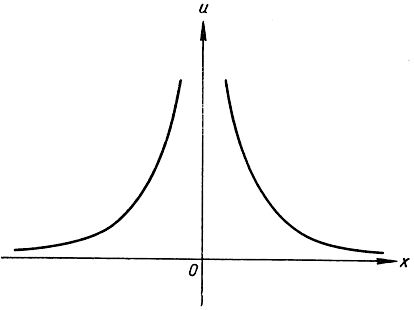
Рис. 158. Разрыв с уходом в бесконечность

Функция f(x), определенная для всех значений х с помощью формул

при х₁ = 0 имеет разрыв другого вида. Здесь существуют пределы и справа, и слева, и они равны между собой, но это общее предельное значение отлично от f(0). Еще иного типа разрыв дается функцией, график которой изображен на рис. 158,

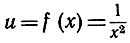
в точке х = 0. Если заставим х стремиться к 0 с любой стороны, то и неизменно будет стремиться к бесконечности, но график функции "прерывается" в этой точке, причем малым изменениям независимого переменного х в окрестности точки х = 0 могут соответствовать очень большие изменения зависимого переменного u. Строго говоря, значение функции не определено при х = 0, поскольку мы не считаем бесконечность числом, и поэтому нельзя говорить, что функция f(x) равна бесконечности при х = 0. Итак, мы говорим только, что функция f(x) "стремится к бесконечности", когда х приближается к нулю.

Совсем иной характер разрыва, наконец, у функции 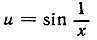в точке х = 0 (рис. 156).

Приведенные примеры показывают несколько различных характерных случаев, когда функция перестает быть непрерывной в некоторой точке x = x₁.

1) Может случиться, что функция станет непрерывной в точке x = x₁ после того, как надлежащим образом будет определено или будет изменено уже определенное значение ее при x = x₁. Например, функция 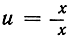постоянно равна 1 при х≠0; она не определена при х = 0, поскольку ⁰/₀ - лишенный смысла символ. Но если в этом примере мы условимся считать, что значение u = 1 соответствует также и значению х = 0, то функция, таким образом "расширенная", становится непрерывной во всех точках без исключения. Тот же результат будет достигнут, если мы изменим значение функции при х = 0 во втором из приведенных выше примеров и вместо f(0) = 1 положим f(0) = 0. Разрывы этого рода называются устранимыми.

2) Функция стремится к различным пределам в зависимости от того, справа или слева х приближается к х₁, как на рис. 157.

3) Не существует предела ни с одной стороны, ни с другой стороны, как на рис. 156.

4) Функция стремится к бесконечности, когда х приближается к x₁ (рис. 158).

Разрывы трех последних типов называются существенными или неустранимыми; они не могут быть устранены с помощью надлежащего определения значения функции в одной лишь точке х = х₁.

Упражнения.

1. Наметить графики функций 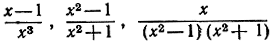и найти точки разрыва.
2. Наметить графики функций 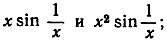проверить, что непрерывность не нарушена в точке х = 0, если принять, что u = 0 при х = 0 в обоих случаях.
3. ^* Показать, что функция 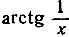имеет разрыв второго типа (скачок) при х = 0.