4. Сложные функции

Вторым важным методом создания новых функций из двух или большего числа данных является составление сложных функций ("композиция"). Так, например, функция

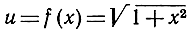
"составлена" из двух простых функций

и может быть записана так:

(читается "h от g от x"). Аналогично функция

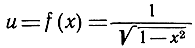
составлена из трех функций

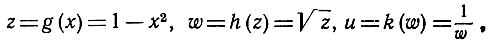
так что можно написать

Функция

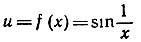
составлена из двух функций

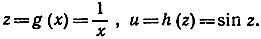
Функция 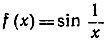не определена при х = 0, так как при х = 0 выражение 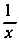не имеет смысла. График этой замечательной функции находится в некоторой связи с графиком синуса. Мы знаем, что sin z = 0 при z = kπ, где k - произвольное положительное или отрицательное целое число. Кроме того,

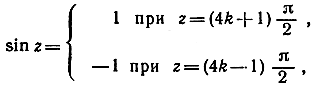
где k - произвольное целое число. Отсюда имеем:

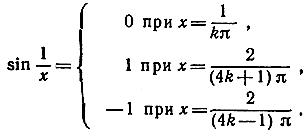
Если мы последовательно станем полагать

знаменатели этих дробей будут возрастать неограниченно и, следовательно, значения х, при которых функция 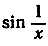имеет значения 1, -1, 0, будут сгущаться все больше и больше около точки х = 0. Между каждой такой точкой и началом будет всегда бесконечное количество колебаний. График этой функции показан на рис. 156.

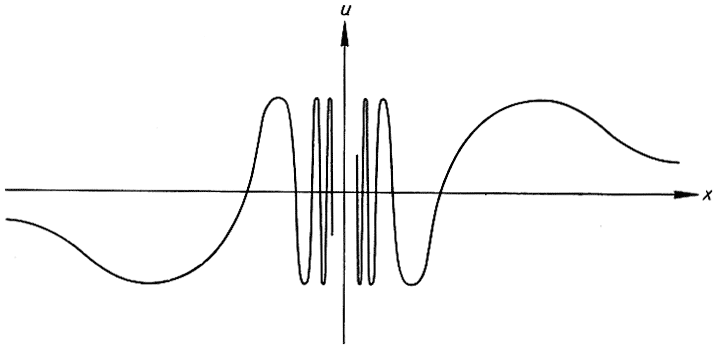
Рис. 156.