3. График функции. Обратные функции

Часто характер функции чрезвычайно ясно выражается с помощью простого графика. Если (х, u) - координаты на плоскости относительно двух взаимно перпендикулярных осей, то линейные функции, а именно

изображаются прямыми линиями; квадратические функции

- параболами; функция

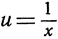
- гиперболой и т. д. По определению график некоторой функции u = f(x) состоит из всех тех точек плоскости, координаты которых (х, u) связаны уравнением u = f(x). Функции sin x, cos x, tg x представлены графически на рис. 151 и 152. Эти графики наглядно показывают, как возрастают или убывают функции при изменении х.

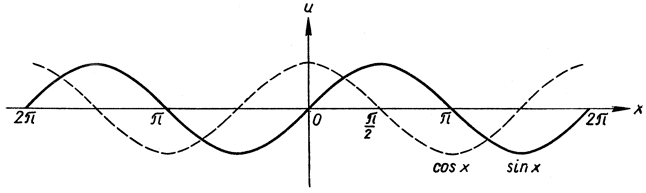
Рис. 151. Графики функций sin x и cos x

Одним из важных методов, служащих для введения новых функций, является следующий. Исходя из некоторой известной функции F(X), можно попытаться решить уравнение U = F(X) относительно X - так, чтобы X было выражено как функция от U:

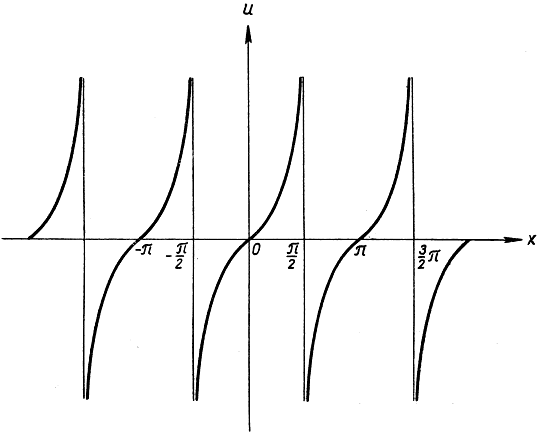
Рис. 152. u = tg x

Тогда функция G(U) называется обратной относительно функции F(X). Этот процесс приводит к результату однозначно только в том случае, если функция U = F(X) определяет взаимно однозначное отображение области изменяемости X на область изменяемости U, т. е. если неравенство Х₁≠Х₂ всегда влечет за собой неравенство F(X₁) ≠ F(X₂). Только при этом условии каждому значению U будет соответствовать единственное значение X. Здесь будет кстати вспомнить приведенный выше пример, в котором роль независимого переменного X играл любой треугольник на плоскости, а в качестве функции U = F(X) рассматривался его периметр. Очевидно, что такое отображение множества S треугольников на множество Т положительных чисел не является взаимно однозначным, так как имеется бесконечное количество различных треугольников с одним и тем же периметром. Итак, в этом случае соотношение U = F(X) не может служить для однозначного определения обратной функции. G другой стороны, функция m = 2n, где n пробегает множество S всех целых чисел, a m - множество Т четных чисел, напротив, дает взаимно однозначное соответствие между двумя множествами, и обратная функция 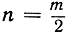будет определена. В качестве другого примера данного однозначного отображения приведем функцию

Когда х пробегает множество всех действительных чисел, u тоже пробегает множество всех действительных чисел, принимая каждое значение один и только один раз. Однозначно определенная в этом примере обратная функция имеет вид:

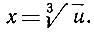
В случае функции

обратная функция не определена однозначно. В самом деле, в силу того что u = х² = (-х)², каждому положительному значению и соответствуют два разных значения ("прообраза") х. Но если под символом У и подразумевать (как это часто и делается) положительное число, квадрат которого есть х, то обратная функция

существует, если только мы условимся, что рассматривать будем лишь положительные значения х и u.

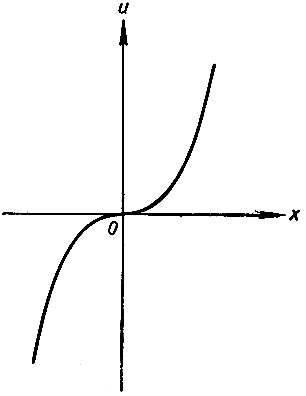
Рис. 153. u = х³

Существование обратной функции может быть сразу установлено при взгляде на график данной функции. Обратная функция существует, определяясь однозначно, в том случае, если каждому значению и соответствует только одно значение х. Геометрически это означает, что нет такой прямой, параллельной оси х, которая пересекала бы график более чем в одной точке. Само собой разумеется, что так будет в том случае, если функция u = f(x) монотонная, т. е. или все время возрастающая, или, наоборот, все время убывающая (при возрастании х). Например, если функция u = f(x) всюду возрастающая, то при х₁<х₂ мы всегда имеем u₁ = f(x₁)< u₂ = f(x₂). Следовательно, для данного значения и существует не более одного значения х, такого, что u = f(x), и обратная функция будет определяться однозначно. График обратной функции х = g(u) получается из данного графика просто путем вращения его на угол в 180° вокруг пунктирной прямой (рис. 154) таким образом, что роли оси х и оси u между собой меняются. Новое положение графика изображает х как функцию от u. В основном положении график указывает значение и как высоты над горизонтальной осью ху в то время как после поворота вновь полученный график указывает значение х как высоты над горизонтальной осью u.

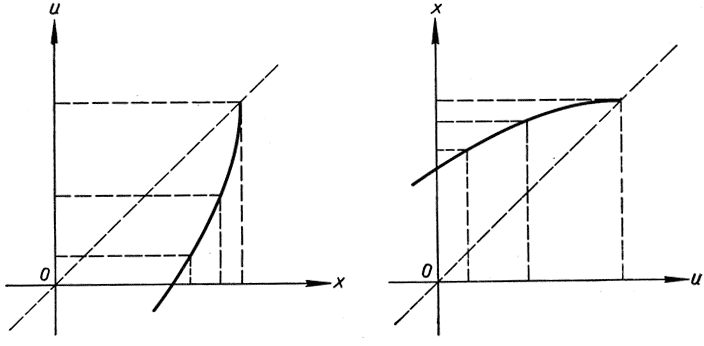
Рис. 154. Взаимно обратные функции

Рассуждения этого параграфа можно иллюстрировать на примере функции

Эта функция монотонна в промежутке 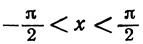(рис. 152): значения u, все время возрастающие вместе с х, изменяются от -∞ до +∞; отсюда ясно, что обратная функция

определена для всех значений u. Эту функцию обозначают arctg u. Таким образом, 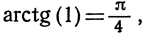поскольку 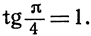График arctg u изображен на рис. 155.

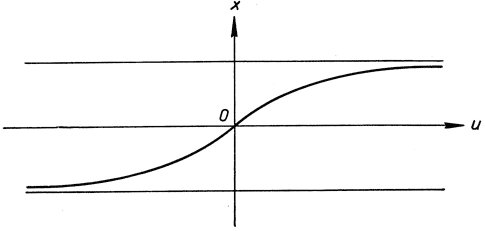
Рис. 155. х = arctg u