2. Радианная мера углов

Во всех практических применениях углы измеряются с помощью единиц, полученных от деления прямого угла на некоторое равное число частей. Если это число равно 90, то единицей измерения является обычный "градус". Деление на 100 частей подходило бы близко к нашей десятичной системе, но принцип измерения при этом оставался бы прежним. В теоретических же применениях выгоднее использовать по существу совершенно другой метод определения величины угла, а именно так называемое радианное измерение. Многие важные формулы, содержащие тригонометрические функции углов, имеют в этой системе измерения более простой вид, чем при измерении углов в градусах.

Для того чтобы найти радианную меру некоторого угла, опишем из вершины этого угла как из центра круг радиуса 1.

Длину дуги s той части нашей окружности, которая расположена между сторонами угла, назовем радианной мерой угла. Так как длина всей окружности единичного радиуса равна 2π, то "полный" угол в 360° имеет радианную меру 2π. Отсюда следует, что если через х обозначить радианную меру угла, а через y его величину в градусах, то х и y связаны соотношением 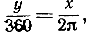или

Так, например, угол в 90° (y = 90) имеет радианной мерой 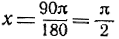и т. д. С другой стороны, угол в 1 радиан (угол, радианной мерой которого является х = 1) есть центральный угол, стягиваемый дугой, длина которой равна радиусу окружности; градусная мера такого угла содержит 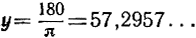градусов. Для того чтобы от радианной меры угла 180х перейти к его градусной мере y, нужно величину х умножить на число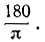

Радианная мера х некоторого угла равна также двойной площади А сектора, вырезаемого этим углом из круга единичного радиуса; в самом деле, эта площадь относится ко всей площади круга так, как длина дуги относится к длине всей окружности: 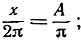итак, х = 2А.

Будем впредь под углом х подразумевать угол, радианная мера которого есть х. Угол, градусное измерение которого равно х, будем в дальнейшем, чтобы устранить всякую неясность, обозначать через х°.

Позднее станет совершенно очевидным, насколько выгодно пользоваться радианным измерением при разного рода аналитических операциях. Однако следует признать, что для практического употребления оно скорее неудобно. В самом деле, так как π - иррациональное число, то, сколько раз мы ни откладывали бы по кругу единичный угол, т. е. угол с радианной мерой, равной 1, мы никогда не вернемся в начальную точку. Обычное же измерение таково, что после откладывания одного градуса 360 раз или 90 градусов 4 раза мы возвращаемся в исходную точку.