§ 1. Независимое переменное и функция

1. Определения и примеры

Нередко приходится иметь дело с математическими объектами, которые мы выбираем свободно, по нашему собственному выбору, из некоторой совокупности (множества) 5. Избираемый объект в таких случаях носит название переменного (или переменной), а совокупность S - области его (ее) изменения. Переменные принято обозначать последними буквами алфавита. Например, если буквой 5 обозначено множество всех целых чисел, то переменное X из области A обозначает некоторое произвольное целое число. Говорят, что "переменное X пробегает множество S", подразумевая, что переменное X мы можем отождествить с любым элементом множества S. Пользоваться понятием переменного удобно, если мы хотим высказать утверждение относительно элементов, которые можно произвольно выбирать из целого множества. Например, если S обозначает, как было указано, множество целых чисел, a X и Y - переменные из области S, то формула

представляет удобное символическое выражение того обстоятельства, что сумма любых двух целых чисел не зависит от порядка слагаемых. Частный случай этого выражен равенством

в котором фигурируют постоянные числа; но, для того чтобы выразить общий закон, справедливый для всех пар чисел, нужно применить символы, имеющие значение переменных.

Нет никакой необходимости в том, чтобы область 5 переменного X была множеством чисел. Например, S может быть множеством всех кругов на плоскости; тогда переменное X будет обозначать любой индивидуальный круг. Или S может быть множеством всех замкнутых многоугольников плоскости, и тогда X - любой индивидуальный многоугольник. Не является также необходимым, чтобы область переменного содержала бесконечное число элементов. Например, X может обозначать любого отдельного человека из населения S данного города в определенный момент времени. Или же X может обозначать любой из возможных остатков при делении целого числа на 5; в этом последнем случае область S состоит из пяти чисел: 0, 1,2, 3, 4.

Наиболее важным оказывается случай числового переменного; в этом случае употребляется обычно маленькая буква х - это тот случай, когда областью изменения S является некоторый интервал (промежуток) a≤x≤b действительной числовой оси. В этом случае говорят, что х есть непрерывное (или действительное) переменное в рассматриваемом интервале. Область изменения непрерывного переменного может простираться и до бесконечности. Так, например, S может быть множеством всех положительных действительных чисел x>0 или даже множеством всех действительных чисел без всякого исключения. Аналогичным образом мы можем рассматривать переменное X, значениями которого являются точки плоскости или некоторой данной области плоскости, подобной внутренности прямоугольника или круга. Так как каждая точка плоскости определяется своими двумя координатами (х, у), взятыми относительно некоторой фиксированной пары осей, то в этом случае часто говорят, что имеют дело с парой действительных (непрерывных) переменных х и y.

Может случиться так, что каждому значению переменного X сопоставляется некоторое определенное значение другого переменного U. Тогда переменное U называется функцией переменного X. Способ, посредством которого U связано с X, выражается символом вроде U = F(X) (читается "равно F от X"). Если X пробегает множество S, то переменное U пробегает некоторое другое множество, скажем, Т. Например, если S есть множество треугольников X на плоскости, то под функцией U = F(X) можно подразумевать длину периметра рассматриваемого треугольника X; Т будет, следовательно, множеством всех положительных чисел. Отметим, что два различных треугольника Х₁и Х₂ свободно могут иметь равные по длине периметры, так что равенство F(X₁) = F(X₂) возможно и в том случае, если Х₁ ≠ Х₂. Проективное преобразование одной плоскости S в некоторую другую - Т ставит в соответствие каждой точке X плоскости .5 единственную точку U плоскости Т согласно определенному правилу, которое можно выразить функциональным символом U - F(X). В этом примере, в противоположность предыдущему, мы имеем всегда неравенство F(X₁) ≠ F(X₂), если только Х₁ ≠ X₂, и мы говорим в связи с этим, что отображение плоскости S на плоскость Т - взаимно однозначное или однооднозначное (см. стр. 215).

Функции непрерывного переменного часто определяются с помощью алгебраических выражений. Примерами могут служить следующие функции:

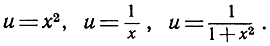
В первом и в последнем из этих выражений х может пробегать множество всех действительных чисел, в то время как во втором примере х может пробегать множество всех действительных чисел, за исключением 0 (значение 0 исключается, так как символ ¹/₀ не есть число).

Число В(n) простых множителей числа n есть функция n, причем n пробегает множество натуральных чисел. Вообще, любую последовательность чисел а₁, а₂, а₃, ... можно рассматривать как множество значений некоторой функции u = F(n), причем областью изменения независимого переменного при этом является множество натуральных чисел. Только ради сокращения записи принято обозначать n-й член последовательности символом а_n, вместо того чтобы употреблять более отчетливое функциональное обозначение F(n). Следующие выражения, о которых говорилось в главе I:

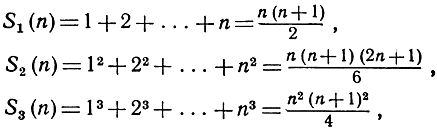
являются функциями целого переменного n.

Пусть дано соотношение U = F(X); переменное X принято называть независимым переменным, а переменное U - зависимым, поскольку его значения зависят от выбора значения X.

Может случиться, что всем значениям переменного X соответствует одно и то же значение переменного U, т. е. что множество Т состоит из одного-единственного элемента. Мы тогда встречаемся с частным случаем, при котором переменное U в сущности не меняется, т. е. U есть постоянное (постоянная, или константа). Мы включим этот случай в общее понятие функции, несмотря на то что начинающему это может показаться странным, так как он склонен полагать, что основное в самой идее функции лежит как раз в изменении переменного U (при изменении переменного X). Но беды не произойдет - а на самом деле это окажется весьма полезным,- если мы постоянное будем рассматривать как частный случай переменного, "область изменения" которого состоит из одного-единственного элемента.

Понятие функциональной зависимости имеет исключительное значение не только в самой "чистой" математике, но также и в практических ее приложениях. Физические законы являются не чем иным, как выражением способа, посредством которого некоторые величины зависят от других, способных изменяться так или иначе. Так, например, высота звука, производимого колеблющейся струной, зависит от ее длины, от ее веса и от степени ее натяжения; давление атмосферы зависит от высоты; энергия пули зависит от ее массы и скорости. Задача физики состоит в точном или приближенном определении природы всех подобного рода зависимостей.

С помощью понятия функции можно дать точную в математическом смысле характеристику движения. Если представить себе, что движущаяся частица сосредоточена в некоторой точке пространства с прямоугольными координатами х, y, z, а переменное t измеряет время, то движение частицы полностью определено заданием координат х, y, z как функций времени:

Примером этого может служить свободное падение частицы по вертикали под действием одной лишь силы тяжести: мы имеем в этом случае соотношения

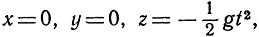
где g обозначает ускорение силы тяжести. Если частица равномерно вращается по единичному кругу в плоскости х, y, то движение ее характеризуется функциями

где ω - постоянное число (так называемая угловая скорость вращения).

Под математической функцией следует понимать просто закон, управляющий взаимными зависимостями переменных величин - и не более того. Понятие функции не подразумевает существования чего-либо близкого к "причине и следствию" в отношениях между независимой и зависимой переменными. Хотя в обыденной речи термин "функциональная зависимость" сплошь и рядом употребляется именно в этом последнем смысле, мы будем избегать такого рода философских интерпретаций. Так, например, закон Бойля, относящийся к газу, заключенному в некоторую замкнутую оболочку при постоянной температуре, утверждает, что произведение давления газа р на его объем v есть величина постоянная, равная с (последнее значение в свою очередь зависит от температуры):

Это соотношение можно решить как относительно р, так и относительно υ:

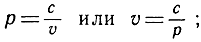
при этом не следует подразумевать ни того, что перемена объема есть "причина" изменения давления, ни того, что изменение давления есть "причина" изменения объема. Для математика существенна лишь форма соответствия (связи) между двумя переменными величинами, которые он рассматривает.

Следует заметить, что подход к понятию функции несколько отличается у математиков и у физиков. Математики обычно подчеркивают закон соответствия, математическую операцию, которую нужно применить к значению независимого переменного х, чтобы получить значение зависимого переменного и. В этом смысле f ( ) есть символ математической операции; значение u = f (х) есть результат применения операции f( ) к числу х. С другой стороны, физик часто более заинтересован в самой величине и, как таковой, чем в какой-либо математической процедуре, с помощью которой значение u может быть получено из значения х. Так, например, сопротивление и воздуха движению предмета зависит от скорости v движения и может быть найдено экспериментальным путем, независимо от того, известна ли явная математическая формула для вычисления u. Физика прежде всего интересует фактическое сопротивление, а не специальная математическая формула f(v), если только эта формула не помогает при анализе поведения величины u. Таково обычно отношение тех, кто применяет математику к физике или инженерному делу. В некоторых высших разделах математического анализа, чтобы избежать путаницы, иногда бывает существенно различать совершенно отчетливо, будет ли под символом u = f (х) подразумеваться операция f ( ), применяемая к х для получения u, или же сама величина u, которая, в свою очередь, может рассматриваться как зависимая, и совсем другим образом, от некоторой другой переменной z. Например, площадь круга задается функцией u = f (х) = πх², где х - радиус круга, но можно также написать: 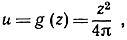понимая под z длину окружности.

Пожалуй, наиболее простым типом математической функции одного независимого переменного являются многочлены (полиномы), имеющие вид

с постоянными "коэффициентами" а₀, а₁, ..., а_n. За ними следуют рациональные функции, такие, как

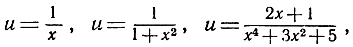
которые являются отношениями многочленов, и затем тригонометрические функции cos x, sin x и 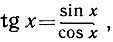которые определяются лучше всего с помощью единичного круга в плоскости ξ, η: ξ² + η² = 1. Если точка Р(ξ, η) движется по этой окружности и если х есть направленный угол, на который нужно повернуть положительную ось х, чтобы она совпала с радиусом OP, то cos х и sin х являются координатами точки Р: cos х = ξ, sin x = η.