*2. Применение к одной механической проблеме

Мы закончим эту главу рассмотрением одной, на первый взгляд трудной, механической проблемы, которая, однако, решается очень просто посредством соображений, связанных с непрерывностью. (Проблема была предложена Г. Уитни.)

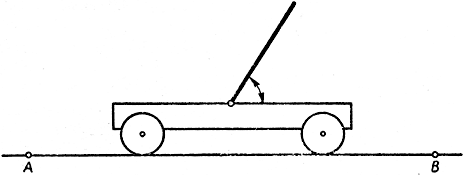
Рис. 175. Проблема Уитни

Предположим, что поезд на протяжении некоторого конечного промежутка времени проходит прямолинейный отрезок пути от станции А до станции В. Вовсе не предполагается, что движение происходите постоянной скоростью или с постоянным ускорением. Напротив, поезд может двигаться как угодно: с ускорениями, с замедлениями; не исключены даже мгновенные остановки или частично даже движение в обратном направлении, прежде чем в итоге поезд придет на станцию В. Но так или иначе движение поезда на протяжении всего временного промежутка считается известным заранее; другими словами, считается заданной функция s = f(t), где s - расстояние поезда от станции A, a t - время, отсчитываемое от момента отправления поезда. К полу одного из вагонов прикреплен на шарнире твердый тяжелый стержень, который без трения может двигаться вокруг оси, параллельной осям вагонов, вперед и назад - от пола до пола. (Мы допускаем, что, прикоснувшись к полу, он в дальнейшем останется на нем лежать, если ему не случится "подпрыгнуть" снова.) Вопрос заключается в следующем: возможно ли в момент отхода поезда поместить стержень в такое начальное положение, т. е. дать ему такой угол наклона, чтобы на протяжении всего пути он не прикоснулся к полу, будучи предоставлен воздействию движения поезда и силе собственной тяжести?

На первый взгляд может показаться совершенно невероятным, чтобы при наперед определенной схеме движения поезда взаимодействие силы тяжести и сил реакции было способно обеспечить требуемое равновесие стержня при единственном условии - надлежащем выборе начального положения. Но мы сейчас установим, что такое начальное положение всегда существует.

К счастью, доказательство не подразумевает точного знания законов динамики. (Исходя из этих законов, решить задачу было бы чрезвычайно трудно.) Достаточно принять только одно допущение физического содержания: последующее движение стержня зависит непрерывно от его начального положения; в частности, если при данном начальном положении стержень во время пути упадет на пол в одну из сторон, то при всяком начальном положении, достаточно мало отличающемся от данного, он не упадет на пол в противоположную сторону.

Обратим теперь внимание на то, что во всякий момент времени положение стержня характеризуется углом α, который он делает с полом. Углам α = 0° и α = 180° соответствуют два взаимно противоположных горизонтальных (лежачих) положения. Обозначим через х значение угла а в начальном положении стержня. Доказательство нашего утверждения будет косвенное, в соответствии с чисто экзистенциальным характером самой проблемы. Допустим, что всегда, т. е. при любом начальном положении стержня, стержень непременно упадет или в одну, или в другую сторону, так что α примет значение или 0°, или 180°. Определим тогда функцию f(x) согласно условию: f(x) = +1 или -1, смотря по тому, упадет ли стержень в сторону, соответствующую углу α = 0° или углу α = 180°. Свойства функции f(x) таковы: она задана в интервале 0≤x≤180°, непрерывна в нем, и притом f(0) = +1, f(180) = -1. Отсюда, по теореме Больцано, следует, что при каком-то промежуточном значении х (0°Eх<180°) должно выполняться равенство f(х) = 0. А это противоречит тому, что функция f(x) может принимать только значения +1 и -1. Значит, приходится отвергнуть сделанное допущение, согласно которому стержень упадет на пол во время движения поезда при каком угодно начальном его положении.

Совершенно ясно, что приведенное доказательство носит чисто теоретический характер, потому что не дает решительно никаких указаний на то, как определить искомое начальное положение стержня. Вместе с тем, даже если бы такое положение и могло быть вычислено теоретически с абсолютной точностью, практически оно было бы бесполезно вследствие своей неустойчивости. Так, например, в предельном случае, если поезд неподвижен в течение всего "путешествия", решение совершенно очевидно: х = 90°; но всякий, кто пытался уравновесить иголку в стоячем положении на гладкой горизонтальной поверхности, понимает, насколько это решение практически нереально. Тем не менее с математической точки зрения приведенное доказательство имеет неоспоримый интерес.

Упражнения.

1. С помощью теоремы на стр. 109-110 установите, что рас" суждение может быть обобщено на случай, когда "путешествие" продолжается бесконечно долго.
2. Обобщите также на случай, когда поезд движется по произвольной кривой на плоскости, а стержень может падать в любом направлении, т. е. стержень обладает двумя степенями свободы. (Указание. Невозможно непрерывно отобразить круговой диск на одну его окружность, оставляя все точки окружности неподвижными - см. стр. 282.)