*3. Основная теорема алгебры

Основная теорема алгебры утверждает, что если функция f(z) имеет вид

где n≥1 и a_n-1, a_n-2, ..., a₁, a₀ - какие угодно комплексные числа, то существует такое комплексное число α, что f(α) = 0. Другими словами, в поле комплексных чисел всякое алгебраическое уравнение имеет корень. (Основываясь на этой теореме, мы на стр. 129 сделали дальнейшее заключение: полином f(z) может быть разложен на n линейных множителей

где α₁, α₂, ..., α_n - нули f(z).) Замечательно, что эту теорему можно доказать, исходя из соображений топологического характера, как и теорему Брауэра о неподвижной точке.

Пусть читатель вспомнит, что комплексное число есть символ вида х + yi, где х и y - действительные числа, а символ i обладает свойством i² = -1. Комплексное число х + yi изображается точкой (х, у) в плоскости прямоугольных координат. Если мы введем в этой же плоскости полярные координаты, принимая начало координат за полюс, а положительное направление оси х за полярную ось, то можно будет написать

где 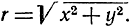Из формулы Муавра следует, что zⁿ = rⁿ(cos nθ + i sin nθ) (см. стр. 124). Отсюда ясно, что если комплексное число z описывает круг радиуса r с центром в начале координат, то zⁿ опишет ровно n раз круг радиусом rⁿ. Напомним еще, что модуль z (обозначаемый через |z|) представляет собой расстояние z от 0 и что если z' = х' + iy', то |z - z'| есть расстояние между z и z'. После этих напоминаний можно перейти к доказательству теоремы.

Допустим, что полином (1) не имеет корней, так что при любом комплексном z

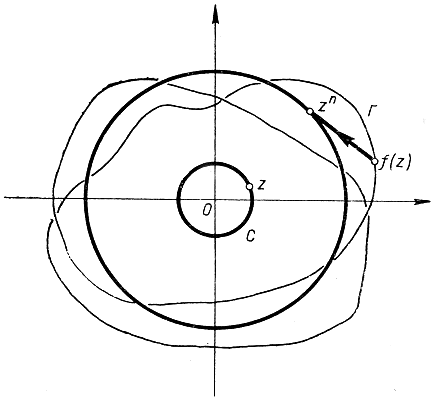
Рис. 150. Доказательство основной теоремы алгебры

При этом допущении, если r описывает некоторую замкнутую кривую в х, y плоскости, то f(z) опишет некоторую замкнутую кривую Г, не проходящую через начало координат (рис. 150). Можно определить порядок точки О для функции f(z) относительно замкнутой кривой С как число полных поворотов, совершаемых вектором, идущим от О к точке f(z) на кривой Г, когда z делает полный обход по кривой С. Возьмем в качестве кривой С окружность с центром О и радиусом t и обозначим через φ(0) порядок точки О для функции f(z) относительно окружности с центром О и радиусом t. Очевидно, φ(0) = 0, так как круг радиуса 0 сводится к одной точке и кривая Г также сводится к одной точке f(0) ≠ 0. Если мы докажем, что при достаточно больших значениях/функция φ(t) равна n, то в этом уже будет заключаться противоречие, так как, с одной стороны, порядок φ(t) должен быть непрерывной функцией t (поскольку f(z) есть непрерывная функция z), а с другой стороны, функция φ(t) может принимать только целые значения и потому никак не может перейти от значения 0 к значению n непрерывно.

Нам остается доказать, что при достаточно больших значениях t

Для этого заметим, что если радиус круга t удовлетворяет неравенствам

то

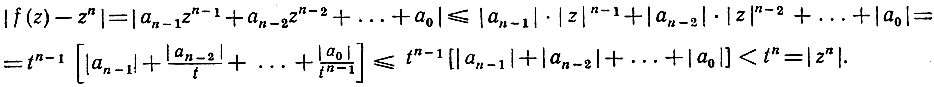
Так как выражение слева есть не что иное, как расстояние между точками zⁿ и f(z), а выражение в самой правой части неравенства - расстояние точки zⁿ от начала координат, то мы видим отсюда, что отрезок, соединяющий точки zⁿ и f (z), не "пройдет через начало координат, если только z будет находиться на круге радиуса t с центром в начале. В таком случае имеется возможность деформировать кривую, описываемую точкой f(z) в кривую, описываемую точкой zⁿ, без прохода через начало, смещая непрерывным движением каждую точку f(z) к соответствующей точке zⁿ по прямолинейному отрезку. При этом порядок начала может принимать только целые значения и вместе с тем во время деформации может меняться не иначе, как непрерывно; значит, для обеих функций f(z) и zⁿ он одинаков, и так как для zⁿ он равен n, то имеет то же самое значение и для f(z). Доказательство закончено.